Question

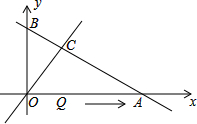
20．如圖，直線y=-$\frac{1}{2}$x+3與坐標軸分別交于A，B兩點，與直線y=x交于點C，線段OA上的點Q以每秒1個單位長度的速度從點O出發向點A作勻速運動，運動時間為t秒，連接CQ．若△OQC是等腰直角三角形，則t的值為 （　　）

• A． 2
• B． 4
• C． 2或3
• D． 2或4

Answer 1

分析 分為兩種情況，畫出圖形，根據等腰三角形的性質求出即可．

解答 解：∵由$\left\{\begin{array}{l}{y=-\frac{1}{2}x+3}\\{y=x}\end{array}\right.$，得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$，
∴C（2，2）；
如圖1，當∠CQO=90°，CQ=OQ，
∵C（2，2），
∴OQ=CQ=2，
∴t=2，
②如圖2，當∠OCQ=90°，OC=CQ，
過C作CM⊥OA于M，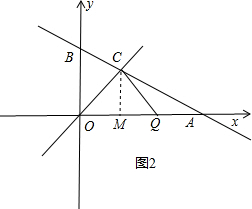
∵C（2，2），
∴CM=OM=2，
∴QM=OM=2，
∴t=2+2=4，
即t的值為2或4，
故選D．

點評 本題考查了用待定系數法求出一次函數解析式，等腰直角三角形等知識點的應用，題目是一道比較典型的題目，綜合性比較強．