
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
分析 先將621分解因數,由于,$\frac{621xy}{x+y}$是整數,得出(x+y)只是621xy的約數,即可得出9個二元不定方程,針對于前8個,x+y是奇數,要使兩個數的和是奇數,這兩個加數中必有一個為偶數,而x,y是質數,偶數中只有2是質數,即,x,y中必有一個是2,求出另一個加數,再判斷它是否是不同的質數,即可得出結論,針對于最后一個,用y表示出x,用x,y都是整數即可求出x,y的值,再判斷是否是不同的質數,即可.
解答 解:621=3×207=9×69=23×27=1×621,
∵$\frac{621xy}{x+y}$是整數,且x,y是互不相同的質數,
∴(x+y)只是621xy的約數,
∴①x+y=3,當x=2時,y=3-x=1,而1不是質數,此種情況不符合題意,
同理:y=2時,也不符合題意,即:此種情況中不存在有序數對(x,y);
②x+y=207,當x=2時,y=207-x=205,而205不是質數,此種情況不符合題意,
同理:y=2時,也不符合題意,即:此種情況中不存在有序數對(x,y);
③x+y=9,∵當x=2時,y=9-x=7,而7是不等于2的質數,
∴有序數對為(2,7),
同理:當y=2時,有序數對為(7,2),共兩種;
④x+y=69,∵當x=2時,y=69-x=67,而67是不等于2的質數,
∴有序數對為(2,67),
同理:當y=2時,有序數對為(67,2),共兩種;
⑤x+y=23,當x=2時,y=23-x=21,而21不是質數,此種情況不符合題意,
同理:y=2時,也不符合題意,即:此種情況中不存在有序數對(x,y);
⑥x+y=27,當x=2時,y=27-x=5,而25不是質數,此種情況不符合題意,
同理:y=2時,也不符合題意,即:此種情況中不存在有序數對(x,y);
⑦x+y=1,∵x,y是互不相同的質數,此種情況不存在兩個質數的和為1;
⑧x+y=621,∵當x=2時,y=621-x=619,而619是不等于2的質數,
∴有序數對為(2,619),
同理:當y=2時,有序數對為(619,2),共兩種;
⑨x+y=xy,∴x=$\frac{y}{y-1}$,
∵x,y是整數數,
∴y-1=1,
∴y=2,
∴x=2,
∵x,y是互不相同的質數,所以舍去.
即:滿足條件的有序數對(x,y)有(2,7),(7,2),(2,67),(67,2),(2,691),(619,2),共6種,
故選B.
點評 此題是質數與合數,主要考查了數的分解因數,一元一次方程的解法,確定出$\frac{621xy}{x+y}$是整數的x,y滿足的條件是解本題的關鍵,而判斷出兩個質數的和是奇數時,必有一個加數是質數2,是解本題的難點,此題用到分類討論的思想,是一道很好的競賽題.


科目:初中數學 來源: 題型:解答題
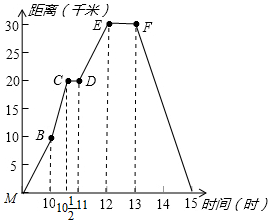 如圖所示,折線表示小麗騎車離家的距離與時間的關系,小麗上午九時離開家,下午十五時到家,根據折線圖所提供的信息,思考并回答下列問題:
如圖所示,折線表示小麗騎車離家的距離與時間的關系,小麗上午九時離開家,下午十五時到家,根據折線圖所提供的信息,思考并回答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1,2,$\sqrt{3}$ | B. | 3,4,5 | C. | 1,1,$\sqrt{2}$ | D. | 6,12,13 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
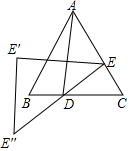 如圖,在等邊△ABC中,AB=4,D是BC邊上任意一點(不與B,C重合),過點D作DE⊥AC,垂足為E,作點E關于直線AD對稱的點E',作點E關于點D的對稱點E″,作△EE'E″,當△EE'E″是軸對稱圖形時,S△EE'E″=48-24$\sqrt{3}$.
如圖,在等邊△ABC中,AB=4,D是BC邊上任意一點(不與B,C重合),過點D作DE⊥AC,垂足為E,作點E關于直線AD對稱的點E',作點E關于點D的對稱點E″,作△EE'E″,當△EE'E″是軸對稱圖形時,S△EE'E″=48-24$\sqrt{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知∠AOB和點C,D,請用直尺和圓規(guī)準確作出點P,使它到∠AOB的兩邊距離相等,且PC=PD.(不寫作法,保留作圖痕跡)
如圖,已知∠AOB和點C,D,請用直尺和圓規(guī)準確作出點P,使它到∠AOB的兩邊距離相等,且PC=PD.(不寫作法,保留作圖痕跡)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 兩個銳角對應相等 | B. | 一個銳角、一條直角邊對應相等 | ||
| C. | 兩條直角邊對應相等 | D. | 一條斜邊、一條直角邊對應相等 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com