
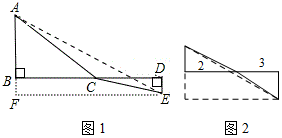
 如圖,C為線段BD上一動點,分別過點B、D作AB⊥BD,ED⊥BD,連接AC、EC.已知AB=5,DE=1,BD=8,設CE=x
如圖,C為線段BD上一動點,分別過點B、D作AB⊥BD,ED⊥BD,連接AC、EC.已知AB=5,DE=1,BD=8,設CE=x分析 (1)若點C不在AE的連線上,根據(jù)三角形中任意兩邊之和>第三邊知,AC+CE>AE,故當A、C、E三點共線時,AC+CE的值最小;
(2)由(1)的結果可作BD=12,過點B作AB⊥BD,過點D作ED⊥BD,使AB=2,ED=3,連接AE交BD于點C,則AE的長即為代數(shù)式$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-24x+153}$的最小值,然后構造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性質可求得AE的值.
解答 解:連接AE交BD于C,故當A、C、E三點共線時,AC+CE的值最小;
∵四邊形BDEF是矩形,
BF=DE=1,EF=BD=8,
AF=AB+BF=5+1=6,
AE=$\sqrt{A{F}^{2}+E{F}^{2}}$=10,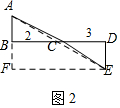
∴AC+CE的最小值是10;
(2)∵$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-24x+153}$=$\sqrt{{x}^{2}+4}$+$\sqrt{(12-x)^{2}+9}$,
如圖2所示,作BD=12,過點B作AB⊥BD,過點D作ED⊥BD,使AB=2,ED=3,
連接AE交BD于點C,設BC=x,則AE的長即為代數(shù)$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-24x+153}$的最小值.
過點A作AF∥BD交ED的延長線于點F,得矩形ABDF,
則AB=DF=2,AF=BD=12,EF=ED+DF=3+2=5,
所以AE=$\sqrt{A{F}^{2}+EF}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
即$\sqrt{{x}^{2}+4}$+$\sqrt{(12-x)^{2}+9}$的最小值為13.
故代數(shù)式$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-24x+153}$的最小值為13.
點評 此題主要考查了軸對稱求最短路線以及勾股定理等知識,本題利用了數(shù)形結合的思想,求形如$\sqrt{{x}^{2}+4}$的式子的最小值,可通過構造直角三角形,利用勾股定理求解.


科目:初中數(shù)學 來源: 題型:填空題
 如圖,將邊長為1的正方形OAPB沿x軸正方向連續(xù)翻轉2016次,點P依次落在點P1,P2,P3,P4,…,P2016的位置,則P2016的坐標為(2015,1).
如圖,將邊長為1的正方形OAPB沿x軸正方向連續(xù)翻轉2016次,點P依次落在點P1,P2,P3,P4,…,P2016的位置,則P2016的坐標為(2015,1).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ | D. | $\frac{\sqrt{18}-\sqrt{8}}{2}$=1 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
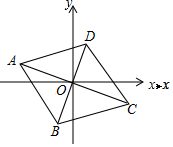 如圖,平行四邊形ABCD的對角線交于坐標原點O.若點A的坐標為(-4,2),則點C坐標為( )
如圖,平行四邊形ABCD的對角線交于坐標原點O.若點A的坐標為(-4,2),則點C坐標為( )| A. | (4,-2) | B. | (4,2) | C. | (2,-4) | D. | (-2,-4) |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
 如圖所示,半徑均為1個單位長度的半圓O1、O2、O3…組成一條平滑的曲線,點P從原點O出發(fā).沿這條曲線向右運動,速度為每秒$\frac{π}{6}$個單位長度,則第2015秒時,點P的坐標是($\frac{1336+\sqrt{3}}{2}$,-$\frac{1}{2}$).
如圖所示,半徑均為1個單位長度的半圓O1、O2、O3…組成一條平滑的曲線,點P從原點O出發(fā).沿這條曲線向右運動,速度為每秒$\frac{π}{6}$個單位長度,則第2015秒時,點P的坐標是($\frac{1336+\sqrt{3}}{2}$,-$\frac{1}{2}$).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com