
分析 分式乘分式,用分子的積作積的分子,分母的積作積的分母;同分母的分式相加減,分母不變,把分子相加減;分式的混合運算,要注意運算順序,式與數(shù)有相同的混合運算順序;先乘方,再乘除,然后加減,有括號的先算括號里面的.
解答 解:(1)$\frac{3x{y}^{2}}{4{z}^{2}}$•$\frac{8{z}^{3}}{y}$
=$\frac{24x{y}^{2}{z}^{3}}{4y{z}^{2}}$
=6xyz;
(2)$\frac{{x}^{2}}{x-y}$+$\frac{{y}^{2}}{y-x}$
=$\frac{{x}^{2}}{x-y}$-$\frac{{y}^{2}}{x-y}$
=$\frac{{x}^{2}-{y}^{2}}{x-y}$
=x+y;
(3)$\frac{1}{x+1}$-$\frac{1}{{x}^{2}-1}$×$\frac{{x}^{2}-2x+1}{x+1}$
=$\frac{1}{x+1}$-$\frac{1}{(x+1)(x-1)}$×$\frac{(x-1)^{2}}{x+1}$
=$\frac{1}{x+1}$-$\frac{x-1}{(x+1)^{2}}$
=$\frac{x+1}{(x+1)^{2}}$-$\frac{x-1}{(x+1)^{2}}$
=$\frac{2}{(x+1)^{2}}$;
(4)(1-$\frac{1}{a+1}$)÷$\frac{{a}^{2}-a}{a+1}$
=$\frac{a+1-1}{a+1}$×$\frac{a+1}{a(a-1)}$
=$\frac{a}{a+1}$×$\frac{a+1}{a(a-1)}$
=$\frac{1}{a-1}$.
點評 本題主要考查了分式加減法,乘除法以及分式混合運算,解題時注意:運算的結(jié)果要化成最簡分式或整式.分子、分母中有公因式的要進行約分化為最簡分式或整式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
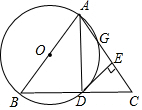 如圖,以等腰三角形ABC的一腰AB為直徑的⊙O交BC于點D,交AC于點G,連結(jié)AD,并過點D作⊙O的切線DE,交AC于點E.求證:
如圖,以等腰三角形ABC的一腰AB為直徑的⊙O交BC于點D,交AC于點G,連結(jié)AD,并過點D作⊙O的切線DE,交AC于點E.求證:查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5個 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
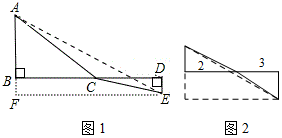 如圖,C為線段BD上一動點,分別過點B、D作AB⊥BD,ED⊥BD,連接AC、EC.已知AB=5,DE=1,BD=8,設(shè)CE=x
如圖,C為線段BD上一動點,分別過點B、D作AB⊥BD,ED⊥BD,連接AC、EC.已知AB=5,DE=1,BD=8,設(shè)CE=x查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
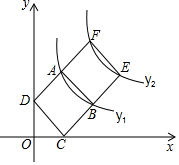 如圖,在邊長均為1的正方形ABCD和ABEF中,頂點A,B在雙曲線y1=$\frac{{k}_{1}}{x}$(k1≠0)上,頂點E,F(xiàn)在雙曲線y2=$\frac{{k}_{2}}{x}$(k2≠0)上,頂點C,D分別在x軸和y軸上,則k1=1,k2=3.
如圖,在邊長均為1的正方形ABCD和ABEF中,頂點A,B在雙曲線y1=$\frac{{k}_{1}}{x}$(k1≠0)上,頂點E,F(xiàn)在雙曲線y2=$\frac{{k}_{2}}{x}$(k2≠0)上,頂點C,D分別在x軸和y軸上,則k1=1,k2=3.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com