
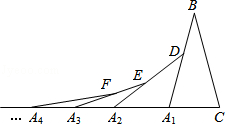
 如圖,在第一個△A1BC中,∠B=30°,A1B=CB,在邊A1B上任取一D,延長CA2到A2,使A1A2=A1D,得到第2個△A1A2D,在邊A2B上任取一點E,延長A1A2到A3,使A2A3=A2E,得到第三個△A2A3E,…按此做法繼續下去,第n個等腰三角形的底角的度數是$\frac{75}{{2}^{n-1}}$度.
如圖,在第一個△A1BC中,∠B=30°,A1B=CB,在邊A1B上任取一D,延長CA2到A2,使A1A2=A1D,得到第2個△A1A2D,在邊A2B上任取一點E,延長A1A2到A3,使A2A3=A2E,得到第三個△A2A3E,…按此做法繼續下去,第n個等腰三角形的底角的度數是$\frac{75}{{2}^{n-1}}$度. 分析 先根據等腰三角形的性質求出∠BA1A的度數,再根據三角形外角的性質及等腰三角形的性質分別求出∠CA2A1,∠DA3A2及∠EA4A3的度數,找出規律即可得出第n個等腰三角形的底角的度數.
解答 解:∵在△ABA1中,∠B=30°,AB=A1B,
∴∠BA1A=$\frac{180°-∠B}{2}$=75°,
∵A1A2=A1D,∠BA1C是△A1A2D的外角,
∴∠DA2A1=$\frac{1}{2}$∠BA1C=$\frac{1}{2}$×75°=37.5°;
同理可得,
∠EA3A2=$\frac{75°}{4}$,∠FA4A3=$\frac{75°}{8}$,
∴第n個等腰三角形的底角的度數=$\frac{75°}{{2}^{n-1}}$.
故答案為$\frac{75}{{2}^{n-1}}$.
點評 本題考查的是等腰三角形的性質及三角形外角的性質,根據題意得出∠DA2A1,∠EA3A2及∠FA4A3的度數,進而找出規律是解答此題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com