
 如圖,C為線段AE上一動點(不與點A,E重合),在AE同側分別作正△ABC和正△CDE,AD與BE交于點O,AD與BC交于點P,BE與CD交于點Q,連接PQ.以下五個結論:
如圖,C為線段AE上一動點(不與點A,E重合),在AE同側分別作正△ABC和正△CDE,AD與BE交于點O,AD與BC交于點P,BE與CD交于點Q,連接PQ.以下五個結論:分析 證明①可先證明△ACD≌△BCE,已有:AB=BC,CD=CE,易得∠ACD=∠BCE,其他的證明需要通過①得到,再利用三角形相似以及等邊三角形的知識分別進行證明即可得出答案.
解答 解:①∵△ABC和△CDE為等邊三角形
∴AC=BC,CD=CE,∠BCA=∠DCB=60°
∴∠ACD=∠BCE
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=CB}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE
∴AD=BE,故①正確;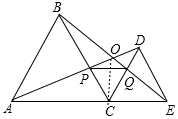
由(1)中的全等得∠CBE=∠DAC,進而可求證△CQB≌△CPA,
∴AP=BQ,故③正確;
又∵∠PCQ=60°可知△PCQ為等邊三角形,
∴∠PQC=∠DCE=60°,
∴PQ∥AE②成立,
∵BC∥DE,
∴∠CBE=∠BED,
∵∠CBE=∠DAE,
∴∠AOB=∠OAE+∠AEO=60°,故⑤正確;
∴∠AOE=120°,
∵∠PBO=∠PAC,∠BOP=∠PCA,
∴△BPO∽△APC,
∴$\frac{PB}{AP}$=$\frac{OP}{PC}$,
∴$\frac{PB}{OP}$=$\frac{AP}{PC}$,∵∠APB=∠CPO,
∴△APB∽△CPO,
∴∠COP=∠ABP=60°,
∴∠COA=∠COB=60°,故④正確,
故正確的有①②③④⑤,
故答案為①②③④⑤.
點評 此題主要考查了等邊三角形的性質、全等三角形的判定與性質、相似三角形的判定與性質,熟練應用三角形全等的證明以及相似三角形的判定是正確解答本題的關鍵.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | 0.5×1011kg | B. | 50×109kg | C. | 5×109kg | D. | 5×1010kg |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
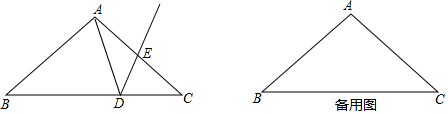
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
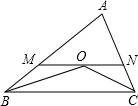 如圖,△ABC中,∠ABC、∠ACB的平分線相交于O,MN過點O且與BC平行.△ABC的周長為20,△AMN的周長為12,則BC的長為( )
如圖,△ABC中,∠ABC、∠ACB的平分線相交于O,MN過點O且與BC平行.△ABC的周長為20,△AMN的周長為12,則BC的長為( )| A. | 10 | B. | 16 | C. | 8 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
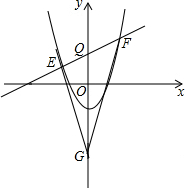 如圖,拋物線y=$\frac{1}{2}$x2-2交y軸于C,不平行于x軸的直線y=kx+3交拋物線于E、F,交y軸于點Q,在y軸的負半軸上是否存在點G使EQ•FG=FQ•EG,若存在,請求出G點坐標;若不存在.請說明理由.
如圖,拋物線y=$\frac{1}{2}$x2-2交y軸于C,不平行于x軸的直線y=kx+3交拋物線于E、F,交y軸于點Q,在y軸的負半軸上是否存在點G使EQ•FG=FQ•EG,若存在,請求出G點坐標;若不存在.請說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com