
分析 (1)首先根據勾股定理求得該直角三角形的斜邊是5,再根據其內切圓的半徑等于兩條直角邊的和與斜邊的差的一半進行計算.
(2)經過圓心O作圓的內接正n邊形的一邊AB的垂線OC,垂足是C.連接OA,則在直角△OAC中,∠AOC=60°,求出∠OAC=30°,由直角三角形的性質求出OC,即可得出OA.
解答 解:(1)根據勾股定理得:直角三角形的斜邊=$\sqrt{{3}^{2}+{4}^{2}}$=5.
∵直角三角形內切圓的半徑等于兩條直角邊的和與斜邊的差的一半,
∴其內切圓的半徑=$\frac{1}{2}$(3+4-5)=1.
故答案為:1.
(2)解:連接中心O和頂點A,作出邊心距OC.如圖所示: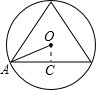 則∠AOC=360÷3÷2=60°,
則∠AOC=360÷3÷2=60°,
∴∠OAC=30°,AC=$\frac{1}{2}$×6=3,
∴OC=$\frac{\sqrt{3}}{3}$AC=$\sqrt{3}$
∴外接圓半徑OA=2OC=2$\sqrt{3}$;
故答案為:2$\sqrt{3}$.
點評 本題考查了勾股定理、三角形的內切圓、三角形的外接圓、等邊三角形的性質、直角三角形的性質;熟練掌握勾股定理和等邊三角形的性質是關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
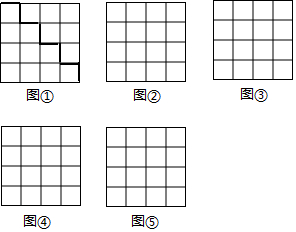 如圖(1),把大小為4×4的正方形方格圖形分割成兩個全等圖形,請在圖中,沿著虛線畫出四種不同的分法,把4×4的正方形方格圖形分割成兩個全等圖形.
如圖(1),把大小為4×4的正方形方格圖形分割成兩個全等圖形,請在圖中,沿著虛線畫出四種不同的分法,把4×4的正方形方格圖形分割成兩個全等圖形.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
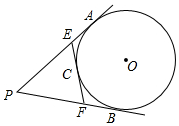 如圖,PA,PB是圓O的切線,切點為分別A,B,圓O的切線EF分別交PA,PB于點E,F,切點C在弧$\widehat{AB}$上,若PA長為2,則△PEF的周長是4.
如圖,PA,PB是圓O的切線,切點為分別A,B,圓O的切線EF分別交PA,PB于點E,F,切點C在弧$\widehat{AB}$上,若PA長為2,則△PEF的周長是4.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=4,⊙B與AB、BC交于E、F,點P是弧$\widehat{EF}$上的一個動點,連接PC,線段PC繞P點逆時針旋轉90°到PD,連接CD,AD.
如圖,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=4,⊙B與AB、BC交于E、F,點P是弧$\widehat{EF}$上的一個動點,連接PC,線段PC繞P點逆時針旋轉90°到PD,連接CD,AD.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com