
【題目】為了解某校“閱讀工程”的開展情況,區教育局從該校初中生中隨機抽取了150名學生進行了閱讀情況的調查問卷,并繪制了如圖所示不完整的統計圖:
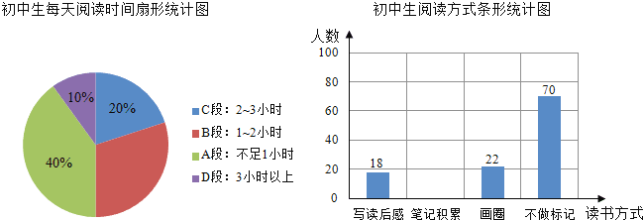
根據上述統計圖提供的信息,回答下列問題:
(1)初中生每天閱讀時間在哪一段的人數最多?每天閱讀時間在B段的扇形的圓心角是多少度?
(2)若將寫讀后感、筆記積累、畫圈點讀三種方式稱為有記憶閱讀,求筆記積累人數占有記憶閱讀人數的百分比,并補全條形統計圖.
【答案】(1)初中生每天閱讀時間不足1小時的人數最多;每天閱讀時間在B段的扇形的圓心角是108°;(2)筆記積累人數占有記憶閱讀人數的百分比為50%,補全條形統計圖見解析.
【解析】
(1)根據扇形統計圖得出每天閱讀時間在不足1小時的人數最多;由總學生數減去其中的求出筆記積累的學生數,求出B段占的百分比,乘以360°即可得到結果;
(2)求出筆記積累占寫讀后感、筆記積累、畫圈點讀三種方式總人數的百分比,補全條形統計圖即可.
解:(1)根據扇形統計圖得:初中生每天閱讀時間不足1小時的人數最多;
閱讀時間在B段的扇形圓心角為(1-10%-20%-40%)×360°=108°;
(2)根據題意得:150-(18+22+70)=40(人),筆記積累學生有40人,
根據題意得:![]() ×100%=50%,
×100%=50%,
則筆記積累人數占有記憶閱讀人數的百分比為50%.
補全條形統計圖,如圖所示.



科目:初中數學 來源: 題型:
【題目】方法感悟:
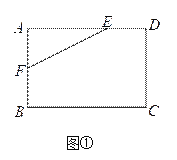
(1)如圖①,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在邊BC、CD上分別存在點G、H,使得四邊形EFGH的周長最小?若存在,求出它周長的最小值;若不存在,請說明理由.
問題解決:
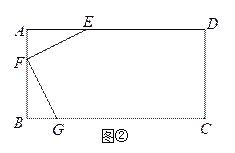
(2)如圖②,有一矩形板材ABCD,AB=3米,AD=6米,現想從此板材中裁出一個面積盡可能大的四邊形EFGH部件,使∠EFG=90°,EF=FG=![]() 米,∠EHG=45°,經研究,只有當點E、F、G分別在邊AD、AB、BC上,且AF<BF,并滿足點H在矩形ABCD內部或邊上時,才有可能裁出符合要求的部件,試問能否裁得符合要求的面積盡可能大的四邊形EFGH部件?若能,求出裁得的四邊形EFGH部件的面積,并寫出在以B為坐標原點,直線BC為x軸,直線BA為y軸的坐標系中,點H的坐標;若不能,請說明理由.
米,∠EHG=45°,經研究,只有當點E、F、G分別在邊AD、AB、BC上,且AF<BF,并滿足點H在矩形ABCD內部或邊上時,才有可能裁出符合要求的部件,試問能否裁得符合要求的面積盡可能大的四邊形EFGH部件?若能,求出裁得的四邊形EFGH部件的面積,并寫出在以B為坐標原點,直線BC為x軸,直線BA為y軸的坐標系中,點H的坐標;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小莉的爸爸買了去看中國籃球職業聯賽總決賽的一張門票,她和哥哥兩人都很想去觀看,可門票只有一張,讀九年級的哥哥想了一個辦法,拿了八張撲克牌,將數字為1,2,3,5的四張牌給小莉,將數字為4,6,7,8的四張牌留給自己,并按如下游戲規則進行:小莉和哥哥從各自的四張牌中隨機抽出一張,然后將抽出的兩張撲克牌數字相加,如果和為偶數,則小莉去;如果和為奇數,則哥哥去.
(1)請用列表的方法求小莉去看中國籃球職業聯賽總決賽的概率;
(2)哥哥設計的游戲規則公平嗎?若公平,請說明理由;若不公平,請你設計一種公平的游戲規則.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校學生利用雙休時間去距學校10 km的天平山社會實踐活動,一部分學生騎電瓶車先走,過了20 min后,其余學生乘公交車沿相同路線出發,結果他們同時到達.已知公交車的速度是電瓶車學生速度的2倍,求騎電瓶車學生的速度和公交車的速度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知O為直線AD上一點,OB是∠AOC內部一條射線且滿足∠AOB與∠AOC互補,OM、ON分別為∠AOC、∠AOB的平分線.
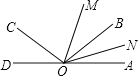
(1)∠COD與∠AOB相等嗎?請說明理由;
(2)若∠AOB=30°,試求∠AOM與∠MON的度數;
(3)若∠MON=55°,試求∠AOC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
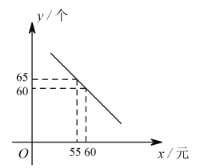
【題目】某體育用品商店試銷一款成本為 50 元的排球,規定試銷期間單價不低于成本價,且獲利不得高于 40%。經試銷發現,銷售量 ![]() (個)與銷售單價
(個)與銷售單價 ![]() (元)之間滿足如圖所示的一次函數關系.
(元)之間滿足如圖所示的一次函數關系.
(1)試確定![]() 與
與 ![]() 之間的函數關系式;
之間的函數關系式;
(2)若該體育用品商店試銷的這款排球所獲得的利潤為 ![]() 元,試寫出利潤
元,試寫出利潤 ![]() (元)與銷售單價
(元)與銷售單價 ![]() (元)之間的函數關系式;當試銷單價定為多少元時,該商店可獲最大利潤?最大利潤是多少元?
(元)之間的函數關系式;當試銷單價定為多少元時,該商店可獲最大利潤?最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
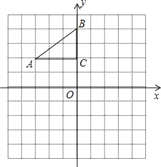
【題目】如圖,在平面直角坐標系中,Rt△ABC的三個頂點分別是A(﹣3,2),B(0,4),C(0,2).
(1)將△ABC以點C為旋轉中心旋轉180°,畫出旋轉后對應的△A1B1C;
(2)平移△ABC,若點A的對應點A2的坐標為(0,﹣4),畫出平移后對應的△A2B2C2 ;
(3)若將△A1B1C繞某一點旋轉可以得到△A2B2C2,請直接寫出旋轉中心的坐標 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果批發市場規定,一次購買蘋果不超過100kg(包括100kg),批發價為5元,如果一次購買100kg以上蘋果,超過100kg的部分蘋果價格打8折.
(I)請填寫下表
購買量/kg | 0 | 50 | 100 | 150 | 200 | … |
付款金額/元 | 0 | 250 | _ | 700 | __ | … |
(Ⅱ)寫出付款金額關于購買量的函數解析式;
(Ⅲ)如果某人付款2100元,求其購買蘋果的數量.
查看答案和解析>>
科目:初中數學 來源: 題型:
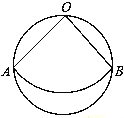
【題目】如圖,從直徑為2cm的圓形紙片中,剪出一個圓心角為90°的扇形OAB,且點O、A、B在圓周上,把它圍成一個圓錐,則圓錐的底面圓的半徑是 cm.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com