
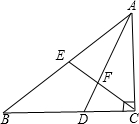
 如圖,△ABC中,∠ACB=90°,D在BC上,E為AB之中點,AD、CE相交于F,且AD=DB.若∠B=35°,求∠DFE的度數.
如圖,△ABC中,∠ACB=90°,D在BC上,E為AB之中點,AD、CE相交于F,且AD=DB.若∠B=35°,求∠DFE的度數. 分析 由直角三角形的性質可求得EC=EB,則可求得∠BEC,由條件利用等腰三角形的性質可求得∠BDA,在四邊形BEFD中利用內角和可求得∠DFE.
解答 解:
∵∠ACB=90°,E為AB之中點,
∴BE=CE,
∴∠B=∠ECB=35°,
∴∠BEC=180°-35°-35°=110°,
∵AD=BD,
∴∠B=∠BAD=35°,
∴∠BDA=180°-35°-35°=110°,
在四邊形BEFD中,
∵∠B+∠BEF+∠BDF+∠DFE=360°,
∴∠DFE=360°-35°-110°-110°=105°.
點評 本題主要考查直角三角形和等腰三角形的性質,利用等腰三角形的性質和直角三角形的性質分別求得∠BDA和∠BEC是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在我市開展的“美麗山城,創衛我同行”活動中,某校倡議八年級學生利用雙休日在各自社區參加義務勞動.為了解同學們勞動情況,學校隨機調查了部分同學的勞動時間,并用得到的數據繪制成不完整的統計圖表,如圖所示:
在我市開展的“美麗山城,創衛我同行”活動中,某校倡議八年級學生利用雙休日在各自社區參加義務勞動.為了解同學們勞動情況,學校隨機調查了部分同學的勞動時間,并用得到的數據繪制成不完整的統計圖表,如圖所示:| 勞動時間(時) | 頻數(人數) | 頻率 |
| 0.5 | 12 | 0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 18 | y |
| 合計 | m | 1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
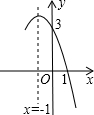 拋物線y=-x2+bx+c的部分圖象如圖所示,對稱軸為x=-1,若y>0,則x的取值范圍是( )
拋物線y=-x2+bx+c的部分圖象如圖所示,對稱軸為x=-1,若y>0,則x的取值范圍是( )| A. | -3<x<1 | B. | x<-3或x>1 | C. | -4<x<l | D. | x<-4或x>1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com