
已知:如圖,在四邊形OABC中,AB∥OC,BC⊥x軸于點C,A(1,﹣1),B(3,﹣1),動點P從點O出發,沿著x軸正方向以每秒2個單位長度的速度移動.過點P作PQ垂直于直線OA,垂足為點Q,設點P移動的時間t秒(0<t<2),△OPQ與四邊形OABC重疊部分的面積為S.
(1)求經過O、A、B三點的拋物線的解析式;
(2)如果將△OPQ繞著點P按逆時針方向旋轉90°,是否存在t,使得△OPQ的頂點O或頂點Q在拋物線上?若存在,請求出t的值;若不存在,請說明理由;
(3)求出S與t的函數關系式.


【考點】二次函數綜合題.
【分析】(1)設拋物線解析式為y=ax2+bx(a≠0),然后把點A、B的坐標代入求出a、b的值,即可得解;
(2)根據旋轉的性質求出點O、Q的坐標,然后分別代入拋物線解析式,求解即可;
(3)求出點Q與點A重合時的t=1,點P與點C重合時的t=1.5,t=2時PQ經過點B,然后分①0<t≤1時,重疊部分的面積等于△POQ的面積,②1<t≤1.5時,重疊部分的面積等于兩個等腰直角三角形的面積的差,③1.5<t<2時,重疊部分的面積等于梯形的面積減去一個等腰直角三角形的面積分別列式整理即可得解.
【解答】解:(1)設拋物線解析式為y=ax2+bx(a≠0),
把點A(1,﹣1),B(3,﹣1)代入得,
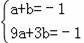
 ,
,
解得: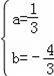
 ,
,
故拋物線解析式為y=
 x2﹣
x2﹣
 x;
x;
(2)如圖1,∵點P從點O出發速度是每秒2個單位長度,
∴OP=2t,
∴點P的坐標為(2t,0),
∵A(1,﹣1),
∴∠AOC=45°,
∴點Q到x軸、y軸的距離都是
 OP=
OP=
 ×2t=t,
×2t=t,
∴點Q的坐標為(t,﹣t);
∵△OPQ繞著點P按逆時針方向旋轉90°,
∴旋轉后點O、Q的對應點的坐標分別為(2t,﹣2t),(3t,﹣t),
若頂點O在拋物線上,則
 ×(2t)2﹣
×(2t)2﹣
 ×(2t)=﹣2t,
×(2t)=﹣2t,
解得:t=
 ,
,
若頂點Q在拋物線上,則
 ×(3t)2﹣
×(3t)2﹣
 ×(3t)=﹣t,
×(3t)=﹣t,
解得:t=1,
綜上所述,存在t=
 或1,使得△OPQ的頂點O或頂點Q在拋物線上;
或1,使得△OPQ的頂點O或頂點Q在拋物線上;
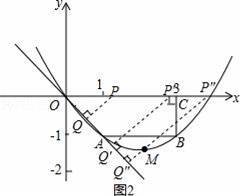
(3)如圖2,點Q與點A重合時,OP=1×2=2,t=2÷2=1,
點P與點C重合時,OP=3,t=3÷2=1.5,
t=2時,OP=2×2=4,PC=4﹣3=1,此時PQ經過點B,
所以,分三種情況討論:
①0<t≤1時,重疊部分的面積等于△POQ的面積,S=
 ×(2t)×
×(2t)×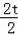
 =t2,
=t2,
②1<t≤1.5時,重疊部分的面積等于兩個等腰直角三角形的面積的差,
S=
 ×(2t)×
×(2t)×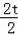
 ﹣
﹣
 ×(
×(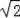
 t﹣
t﹣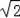
 )2=2t﹣1;
)2=2t﹣1;
③1.5<t<2時,重疊部分的面積等于梯形的面積減去一個等腰直角三角形的面積
S=
 ×(2+3)×1﹣
×(2+3)×1﹣
 ×[1﹣(2t﹣3)]2=﹣2(t﹣2)2+
×[1﹣(2t﹣3)]2=﹣2(t﹣2)2+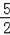
 ;
;
所以,S與t的關系式為S=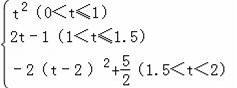
 .
.



【點評】此題主要考查了二次函數綜合題型,主要利用了待定系數法求二次函數解析式,等腰直角三角形的性質,二次函數圖象上點的坐標特征,三角形的面積,難點在于(3)隨著運動時間的變化,根據重疊部分的形狀的不同分情況討論,作出圖形更形象直觀.


 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:初中數學 來源: 題型:
如果單項式5mxay與﹣5nx2a﹣3y是關于x、y的單項式,且它們是同類項.求
(1)(7a﹣22)2013的值;
(2)若5mxay﹣5nx2a﹣3y=0,且xy≠0,求(5m﹣5n)2014的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
反比例函數y=
 的圖象如圖所示,以下結論正確的是( )
的圖象如圖所示,以下結論正確的是( )
①常數m<1;
②y隨x的增大而減小;
③若A為x軸上一點,B為反比例函數上一點,則S△ABC=
 ;
;
④若P(x,y)在圖象上,則P′(﹣x,﹣y)也在圖象上.


A.①②③ B.①③④ C.①②③④ D.①④
查看答案和解析>>
科目:初中數學 來源: 題型:
平面直角坐標系xOy中,點A、B分別在函數y1=
 (x>0)與y2=﹣
(x>0)與y2=﹣
 (x<0)的圖象上,A、B的橫坐標分別為
(x<0)的圖象上,A、B的橫坐標分別為
a、b.


(1)若AB∥x軸,求△OAB的面積;
(2)若△OAB是以AB為底邊的等腰三角形,且a+b≠0,求ab的值;
(3)作邊長為3的正方形ACDE,使AC∥x軸,點D在點A的左上方,那么,對大于或等于4的任意實數a,CD邊與函數y1=
 (x>0)的圖象都有交點,請說明理由.
(x>0)的圖象都有交點,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com