
平面直角坐標系xOy中,點A、B分別在函數y1=
 (x>0)與y2=﹣
(x>0)與y2=﹣
 (x<0)的圖象上,A、B的橫坐標分別為
(x<0)的圖象上,A、B的橫坐標分別為
a、b.


(1)若AB∥x軸,求△OAB的面積;
(2)若△OAB是以AB為底邊的等腰三角形,且a+b≠0,求ab的值;
(3)作邊長為3的正方形ACDE,使AC∥x軸,點D在點A的左上方,那么,對大于或等于4的任意實數a,CD邊與函數y1=
 (x>0)的圖象都有交點,請說明理由.
(x>0)的圖象都有交點,請說明理由.
【考點】反比例函數綜合題.
【專題】代數幾何綜合題;壓軸題.
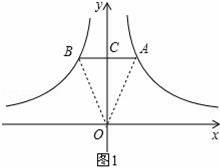
【分析】(1)如圖1,AB交y軸于C,由于AB∥x軸,根據k的幾何意義得到S△OAC=2,S△OBC=2,所以S△OAB=S△OAC+S△OBC=4;
(2)根據函數圖象上點的坐標特征得A、B的縱坐標分別為
 、﹣
、﹣
 ,根據兩點間的距離公式得到OA2=a2+(
,根據兩點間的距離公式得到OA2=a2+(
 )2,OB2=b2+(﹣
)2,OB2=b2+(﹣
 )2,則利用等腰三角形的性質得到a2+(
)2,則利用等腰三角形的性質得到a2+(
 )2=b2+(﹣
)2=b2+(﹣
 )2,變形得到(a+b)(a﹣b)(1﹣
)2,變形得到(a+b)(a﹣b)(1﹣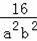
 )=0,由于a+b≠0,a>0,b<0,所以1﹣
)=0,由于a+b≠0,a>0,b<0,所以1﹣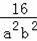
 =0,易得ab=﹣4;
=0,易得ab=﹣4;
(3)由于a≥4,AC=3,則可判斷直線CD在y軸的右側,直線CD與函數y1=
 (x>0)的圖象一定有交點,設直線CD與函數y1=
(x>0)的圖象一定有交點,設直線CD與函數y1=
 (x>0)的圖象交點為F,由于A點坐標為(a,
(x>0)的圖象交點為F,由于A點坐標為(a,
 ),正方形ACDE的邊長為3,則得到C點坐標為(a﹣3,
),正方形ACDE的邊長為3,則得到C點坐標為(a﹣3,
 ),F點的坐標為(a﹣3,
),F點的坐標為(a﹣3,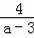
 ),所以FC=
),所以FC=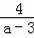
 ﹣
﹣
 ,然后比較FC與3的大小,由于3﹣FC=3﹣(
,然后比較FC與3的大小,由于3﹣FC=3﹣(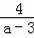
 ﹣
﹣
 )=
)=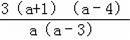
 ,而a≥4,所以3﹣FC≥0,于是可判斷點F在線段DC上.
,而a≥4,所以3﹣FC≥0,于是可判斷點F在線段DC上.
【解答】解:(1)如圖1,AB交y軸于C,
∵AB∥x軸,
∴S△OAC=
 ×|4|=2,S△OBC=
×|4|=2,S△OBC=
 ×|﹣4|=2,
×|﹣4|=2,
∴S△OAB=S△OAC+S△OBC=4;
(2)∵A、B的橫坐標分別為a、b,
∴A、B的縱坐標分別為
 、﹣
、﹣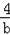
 ,
,
∴OA2=a2+(
 )2,OB2=b2+(﹣
)2,OB2=b2+(﹣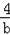
 )2,
)2,
∵△OAB是以AB為底邊的等腰三角形,
∴OA=OB,
∴a2+(
 )2=b2+(﹣
)2=b2+(﹣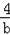
 )2,
)2,
∴a2﹣b2+(
 )2﹣(
)2﹣(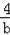
 )2=0,
)2=0,
∴a2﹣b2+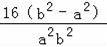
 =0,
=0,
∴(a+b)(a﹣b)(1﹣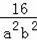
 )=0,
)=0,
∵a+b≠0,a>0,b<0,
∴1﹣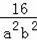
 =0,
=0,
∴ab=﹣4;
(3)∵a≥4,
而AC=3,
∴直線CD在y軸的右側,直線CD與函數y1=
 (x>0)的圖象一定有交點,
(x>0)的圖象一定有交點,
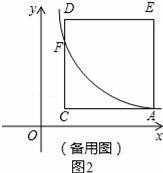
設直線CD與函數y1=
 (x>0)的圖象交點為F,如圖2,
(x>0)的圖象交點為F,如圖2,
∵A點坐標為(a,
 ),正方形ACDE的邊長為3,
),正方形ACDE的邊長為3,
∴C點坐標為(a﹣3,
 ),
),
∴F點的坐標為(a﹣3,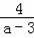
 ),
),
∴FC=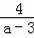
 ﹣
﹣
 ,
,
∵3﹣FC=3﹣(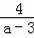
 ﹣
﹣
 )=
)=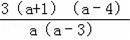
 ,
,
而a≥4,
∴3﹣FC≥0,即FC≤3,
∵CD=3,
∴點F在線段DC上,
即對大于或等于4的任意實數a,CD邊與函數y1=
 (x>0)的圖象都有交點.
(x>0)的圖象都有交點.


【點評】本題考查了反比例函數的綜合題:掌握反比例函數圖象上點的坐標特征、反比例函數比例系數的幾何意義、圖形與坐標和正方形的性質;會利用求差法對代數式比較大小.


科目:初中數學 來源: 題型:
如圖1,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等邊三角形,E是AB的中點,連接CE并延長交AD于F.
(1)求證:①△AEF≌△BEC;②四邊形BCFD是平行四邊形;
(2)如圖2,將四邊形ACBD折疊,使D與C重合,HK為折痕,求sin∠ACH的值.


查看答案和解析>>
科目:初中數學 來源: 題型:
已知:如圖,在四邊形OABC中,AB∥OC,BC⊥x軸于點C,A(1,﹣1),B(3,﹣1),動點P從點O出發,沿著x軸正方向以每秒2個單位長度的速度移動.過點P作PQ垂直于直線OA,垂足為點Q,設點P移動的時間t秒(0<t<2),△OPQ與四邊形OABC重疊部分的面積為S.
(1)求經過O、A、B三點的拋物線的解析式;
(2)如果將△OPQ繞著點P按逆時針方向旋轉90°,是否存在t,使得△OPQ的頂點O或頂點Q在拋物線上?若存在,請求出t的值;若不存在,請說明理由;
(3)求出S與t的函數關系式.


查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,已知△ABC是等腰直角三角形,CD是斜邊AB的中線,△ADC繞點D旋轉一定角度得到△A'DC',A'D交AC于點E,DC'交BC于點F,連接EF,若
 ,則
,則
 = .
= .


查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,半徑為2cm,圓心角為90°的扇形OAB中,分別以OA、OB為直徑作半圓,則圖中陰影部分的面積為( )


A.(
 ﹣1)cm2 B.(
﹣1)cm2 B.(
 +1)cm2 C.1cm2 D.
+1)cm2 C.1cm2 D.
 cm2
cm2
查看答案和解析>>
科目:初中數學 來源: 題型:
我們約定a b=10a×10b,如:2
b=10a×10b,如:2 3=102×103=105,那么4
3=102×103=105,那么4 8為( )
8為( )
A. 32; B. 1032; C. 1012; D. 1210;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com