
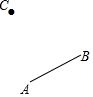
 已知AB是⊙O的弦,點C為圓上一點.
已知AB是⊙O的弦,點C為圓上一點.分析 (1)連結AC,分別作AB、AC的中垂線,交點即為圓心O,然后以O為圓心,OA為半徑作圓即可;
(2)AB的中垂線與⊙O交點分別為E1、E2,△ABE1與△ABE2均為以AB為底的圓的內接等腰三角形;
(3)由R=5,AB=8,根據勾股定理易得AB對應的弦心距為3,進而得到h=5+3=8或h=5-3=2.
解答 解:(1)如圖所示,連結AC,分別作AB、AC的中垂線,交點即為圓心O,然后以O為圓心,OA為半徑作圓即可;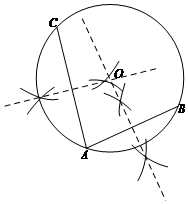
(2)如圖所示,若AB的中垂線與⊙O交點分別為E1、E2,
則△ABE1與△ABE2均為以AB為底的圓的內接等腰三角形;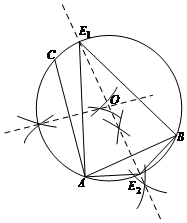
(3)由圓的半徑R=5,AB=8,由勾股定理可得AB對應的弦心距為3,
∴△ABE1中,h=5+3=8;
△ABE2中,h=5-3=2.
點評 本題主要考查了等腰三角形的性質,三角形的外接圓與外心的運用,解決問題時注意:找一個三角形的外心,就是找一個三角形的兩條邊的垂直平分線的交點,三角形的外接圓只有一個.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:選擇題
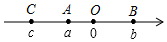 如圖,點A、B、C在數軸上表示的數分別為a、b、c,且OA+OB=OC,則下列結論中:
如圖,點A、B、C在數軸上表示的數分別為a、b、c,且OA+OB=OC,則下列結論中:| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
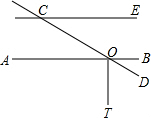
| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2017屆湖北省襄陽市九年級下學期第一次月考數學試卷(解析版) 題型:填空題
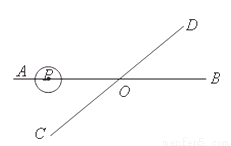
如圖,直線AB、CD相交于點O,∠AOC=300,半徑為1cm的⊙P的圓心在射線OA上,開始時,PO=6cm.如果⊙P以1cm/秒的速度沿由A向B的方向移動,那么當⊙P的運動時間t(秒)滿足條件____________時,⊙P與直線CD相交.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com