
分析 (1)首先通分,然后利用同分母的分式的加減法則求解;
(2)根據A和B兩個式子的值相等,即可列方程求解.
解答 解:(1)A-B=$\frac{2}{x-1}-\frac{x}{{{x^2}-1}}$
=$\frac{2(x+1)-x}{{{x^2}-1}}$
=$\frac{2x+2-x}{{{x^2}-1}}$
=$\frac{x+2}{{{x^2}-1}}$
(2)∵A=B
∴$\frac{2}{x-1}=\frac{x}{{{x^2}-1}}$
去分母,得2(x+1)=x
去括號,得2x+2=x
移項、合并同類項,得x=-2
經檢驗x=-2是原方程的解.
點評 本題考查了分式的加減以及分式方程的解法,解分式方程時一定要注意檢驗.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
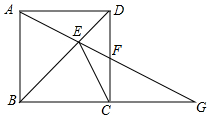 如圖,ABCD是正方形,G是BC延長線上一點,AG交BD于E,交CD于F,求證:CE與△CFG的外接圓相切.
如圖,ABCD是正方形,G是BC延長線上一點,AG交BD于E,交CD于F,求證:CE與△CFG的外接圓相切.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
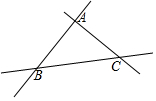 如圖是三條兩兩相交的筆直公路,現欲修建一個加油站,使它到三條公路的距離相等,這個加油站應建在( )
如圖是三條兩兩相交的筆直公路,現欲修建一個加油站,使它到三條公路的距離相等,這個加油站應建在( )| A. | △ABC三邊的中線的交點上 | B. | △ABC三邊垂直平分線的交點上 | ||
| C. | △ABC三條邊高的交點上 | D. | △ABC三內角平分線的交點上 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com