
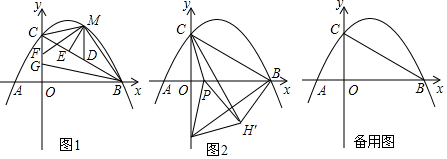
 .
. 分析 (1)利用待定系數(shù)法,把問題轉(zhuǎn)化為方程組解決即可.
(2)如圖1中,延長MD交c軸于H.首先證明△DEM是含有30度角的特殊直角三角形,DM最大時,△DME的周長最大,構(gòu)建二次函數(shù)求出點M的坐標(biāo),將點B向上平移$\frac{\sqrt{3}}{2}$個單位得到點P(6,$\frac{\sqrt{3}}{2}$),作點P關(guān)于y軸的對稱點P′(-6,$\frac{\sqrt{3}}{2}$),連接P′M交y軸于F,此時四邊形BGFM的周長最小.
(3)分四種情形討論①如圖3中,當(dāng)HH′=BH′時,②如圖4中,當(dāng)PH=PH′時,③如圖5中,當(dāng)HB=HH′時,④如圖6中,當(dāng)HH′=BH′時,分別求出OP的長即可解決問題.
解答 解:(1)∵拋物線y=-$\frac{\sqrt{3}}{6}$x2+bx+c與x軸交于A(-2,0)、B(6,0),
∴拋物線的解析式為拋物線y=-$\frac{\sqrt{3}}{6}$(x+2)(x-6)=-$\frac{\sqrt{3}}{6}$x2+$\frac{2}{3}$$\sqrt{3}$x+2$\sqrt{3}$.
∴C(0,2$\sqrt{3}$),
設(shè)直線BC的解析式為y=kx+b則有$\left\{\begin{array}{l}{b=2\sqrt{3}}\\{6k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=2\sqrt{3}}\end{array}\right.$,
∴直線BC的解析式為y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$.
(2)如圖1中,延長MD交c軸于H.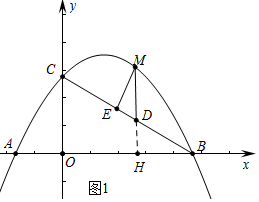
∵tan∠CBO=$\frac{CO}{BO}$=$\frac{\sqrt{3}}{3}$,
∴∠CBO=30°,
∵M(jìn)H⊥OB,
∴∠BHD=90°,
∴∠BDH=∠EDM=60°,
∵M(jìn)E⊥BC,
∴∠EMD=30°,
∴當(dāng)DM的值最大時,△EMD的周長最大,設(shè)M(m,-$\frac{\sqrt{3}}{6}$m2+$\frac{2}{3}$$\sqrt{3}$m+2$\sqrt{3}$)則D(m,-$\frac{\sqrt{3}}{3}$m+2$\sqrt{3}$),
∴MD=-$\frac{\sqrt{3}}{6}$m2+$\frac{2}{3}$$\sqrt{3}$m+2$\sqrt{3}$+$\frac{\sqrt{3}}{3}$m-2$\sqrt{3}$=-$\frac{\sqrt{3}}{6}$m2+$\sqrt{3}$m=-$\frac{\sqrt{3}}{6}$(m-3)2+$\frac{3\sqrt{3}}{2}$,
∵-$\frac{\sqrt{3}}{6}$<0,
∴m=3時,MD有最大值,此時點M(3,$\frac{5\sqrt{3}}{2}$).
如圖2中,∵點F(0,a+$\frac{\sqrt{3}}{2}$),G(0,a),∴FG=$\frac{\sqrt{3}}{2}$.
將點B向上平移$\frac{\sqrt{3}}{2}$個單位得到點P(6,$\frac{\sqrt{3}}{2}$),作點P關(guān)于y軸的對稱點P′(-6,$\frac{\sqrt{3}}{2}$),連接P′M交y軸于F,此時四邊形BGFM的周長最小.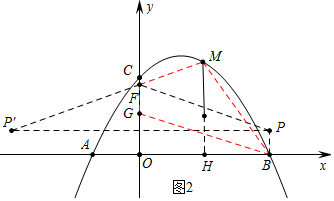
∵直線P′M的解析式為y=$\frac{2}{9}$$\sqrt{3}$x+$\frac{11}{6}$$\sqrt{3}$,
∴F(0,$\frac{11}{6}$$\sqrt{3}$),
∴四邊形BGFM的周長最小值=BG+FG+FM+BM=PF+FG+FM+BM=P′F+FM+FG+BM=P′M+FG+BM=$\sqrt{93}$+$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{111}}{2}$.
(3)①如圖3中,當(dāng)HH′=BH′時,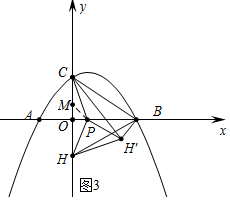
易知∠HCH′=∠H′CB=30°,
∴∠PCO=∠PCH′=15°,在OC上取一點M,使得CM=PM,則∠PMO=30°,設(shè)OP=x,則PM=CM=2x,OM=$\sqrt{3}$x,
則有2x+$\sqrt{3}$x=2$\sqrt{3}$,
∴x=4$\sqrt{3}$-6,
∴P(4$\sqrt{3}$-6,0).
②如圖4中,當(dāng)PH=PH′時,易知點P與點B重合,此時P(6,0).
③如圖5中,當(dāng)HB=HH′時,易知點H′在x軸上.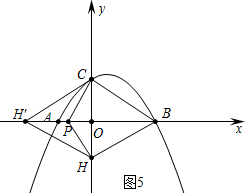
易知∠PCO=30°,OP=OC•tan30°=2,此時P(-2,0).
④如圖6中,當(dāng)HH′=BH′時,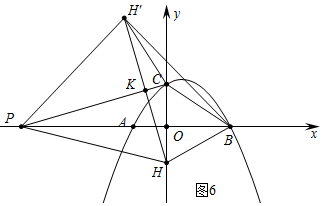
易知∠CHH′=∠CH′H=15°,
∵PH′=PH,CH′=CH,
∴PC⊥HH′于K,
∴∠CPO+∠PCO=90°,∵∠HCK=75°,
∴∠CPO=15°,
在OP上取一點Q,使得PQ=CQ,則∠CQO=30°,PQ=CQ=2OC=4$\sqrt{3}$,OQ=$\sqrt{3}$CO=6,
∴OP=4$\sqrt{3}$+6,
∴P(-4$\sqrt{3}$-6,0).
綜上所述,滿足條件的點P的坐標(biāo)為(4$\sqrt{3}$-6,0)或(6,0)或(-2,0)或(-4$\sqrt{3}$-6,0).
點評 本題考查二次函數(shù)綜合題、最值問題、軸對稱最短問題、一次函數(shù)的應(yīng)用、等腰三角形的判定和性質(zhì)等知識,解題的關(guān)鍵是學(xué)會用轉(zhuǎn)化的思想思考問題,學(xué)會構(gòu)建二次函數(shù)解決最值問題,學(xué)會利用對稱解決最短問題,本題體現(xiàn)了分類討論的數(shù)學(xué)思想,屬于中考壓軸題.


 陽光課堂同步練習(xí)系列答案
陽光課堂同步練習(xí)系列答案科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 5個 | B. | 8個 | C. | 9個 | D. | 19個 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
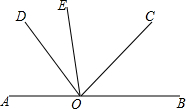 如圖,已知,A、O、B在同一條線上,∠AOE=∠COD,∠EOD=30°.
如圖,已知,A、O、B在同一條線上,∠AOE=∠COD,∠EOD=30°.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 已知點A、B、C、D、E、F是半徑為r的⊙O的六等分點,分別以A、D為圓心,AE和DF長為半徑畫圓弧交于點P.以下說法正確的是( )
已知點A、B、C、D、E、F是半徑為r的⊙O的六等分點,分別以A、D為圓心,AE和DF長為半徑畫圓弧交于點P.以下說法正確的是( )| A. | ①④ | B. | ②③ | C. | ③④ | D. | ①③④ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 若a>0,b>0,則a+b>0 | B. | 對頂角相等 | ||
| C. | 全等三角形的對應(yīng)角相等 | D. | 平行四邊形的兩組對邊分別相等 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com