設凸四邊形ABCD的對角線相交于點O,且AD∥BC,則下面的四個命題:
①已知AB+BC=AD+DC,則ABCD為平行四邊形
②已知DC+DO=AO+AB,則ABCD為平行四邊形
③已知BC+BO+AO=AD+DO+CO,則ABCD為平行四邊形
④已知AD+CO=BC+AO,則ABCD為平行四邊形
其中正確命題的序號是________.(可以多選)
①、③、④
分析:①延長AD到F使得DF=DC,延長CB到E使得BE=AB,通過求證四邊形AECF是平行四邊形,即可推出∠E=∠F,∠EAF=∠ECF,其次根據∠E=∠BAE,∠F=∠DCF,推出∠BAE=∠DCF,即可求出∠BAD=∠BCD,再由∠BCA=∠DAC,求出∠BAC=∠DCA,即可推出AB∥CD,最后由對邊分別平行即可推出四邊形ABCD為平行四邊形,②首先假設命題中的結論成立,根據平行四邊形的性質推出AB=CD,OA=OC,根據等式的性質得到等式DC+CO=AO+AB,而不是題設中的DC+DO=AO+AB,由此推出假設不成立,③首先假設四邊形ABCD為平行四邊形,根據平行四邊形的性質推出AD=BC,AB=CD,OA=OC,OB=OD,
根據等式的性質可推出BC+BO+AO=AD+DO+CO,由此可得假設成立,④首先假設四邊形ABCD為平行四邊形,根據平行四邊形的性質推出AD=BC,OA=OC,根據等式的性質可推出AD+CO=BC+AO,由此可得假設成立.
解答:①延長AD到F使得DF=DC,延長CB到E使得BE=AB,
∴∠E=∠BAE,∠F=∠DCF,
∵AB+BC=AD+DC,
即BE+BC=AD+DF,
∴AF=CE,
∵AD∥BC,

∴AF∥CE,∠BCA=∠DAC,
∴四邊形AECF是平行四邊形,
∴∠E=∠F,∠EAF=∠ECF,
∵∠E=∠BAE,∠F=∠DCF,
∴∠BAE=∠DCF,
∴∠BAD=∠BCD,
∵∠BCA=∠DAC,
∴∠BAC=∠DCA,
∴AB∥CD,
∴四邊形ABCD為平行四邊形,
∴本項正確,

②假設四邊形ABCD是平行四邊形,
∴AB=CD,OA=OC,
∴DC+CO=AO+AB,
∵DC+DO=AO+AB,
∴假設不成立,
∴本項錯誤;
③假設四邊形ABCD為平行四邊形,

∴AD=BC,AB=CD,OA=OC,OB=OD,
∴BC+BO+AO=AD+DO+CO,
∴假設成立,
∴本項正確,
④假設四邊形ABCD為平行四邊形,
∴AD=BC,OA=OC,

∴AD+CO=BC+AO,
∴假設成立,
∴本項正確,
故答案為①③④.
點評:本題主要考查平行四邊形的性質,利用反證法證明命題等知識點,關鍵在于正確的做出輔助線,熟練掌握平行四邊形的性質和判定定理.

 ∴AF∥CE,∠BCA=∠DAC,
∴AF∥CE,∠BCA=∠DAC, ②假設四邊形ABCD是平行四邊形,
②假設四邊形ABCD是平行四邊形, ∴AD=BC,AB=CD,OA=OC,OB=OD,
∴AD=BC,AB=CD,OA=OC,OB=OD, ∴AD+CO=BC+AO,
∴AD+CO=BC+AO,

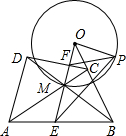 設凸四邊形ABCD的對角線AC、BD的交點為M,過點M作AD的平行線分別交AB、CD于點E、F,交BC的延長線于點O,P是以O為圓心OM為半徑的圓上一點(位置如圖所示),求證:∠OPF=∠OEP.
設凸四邊形ABCD的對角線AC、BD的交點為M,過點M作AD的平行線分別交AB、CD于點E、F,交BC的延長線于點O,P是以O為圓心OM為半徑的圓上一點(位置如圖所示),求證:∠OPF=∠OEP. 設凸四邊形ABCD的對角線AC、BD的交點為M,過點M作AD的平行線分別交AB、CD于點E、F,交BC的延長線于點O,P是以O為圓心OM為半徑的圓上一點(位置如圖所示),求證:∠OPF=∠OEP.
設凸四邊形ABCD的對角線AC、BD的交點為M,過點M作AD的平行線分別交AB、CD于點E、F,交BC的延長線于點O,P是以O為圓心OM為半徑的圓上一點(位置如圖所示),求證:∠OPF=∠OEP.