
如圖12, 已知二次函數的圖像過點O(0,0), A(4,0),B(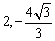 ),M是OA的中點.
),M是OA的中點.
(1)求此二次函數的解析式;
(2)設P是拋物線上的一點,過P作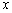 軸的平行線與拋物線交于另一點Q,要使四邊形PQAM是菱形,求P點的坐標;
軸的平行線與拋物線交于另一點Q,要使四邊形PQAM是菱形,求P點的坐標;
|
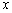 軸下方的部分沿
軸下方的部分沿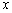 軸向上翻折,得曲線OB′A(B′為B關于
軸向上翻折,得曲線OB′A(B′為B關于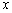 軸的對稱點),在原拋物線
軸的對稱點),在原拋物線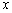 軸的上方部分取一點C,連接CM,CM與翻折后的曲線OB′A交于點D,若△CDA的面積是△MDA面積的2倍,這樣的點C是否存在?若存在求出C點的坐標,若不存在,請說明理由.
軸的上方部分取一點C,連接CM,CM與翻折后的曲線OB′A交于點D,若△CDA的面積是△MDA面積的2倍,這樣的點C是否存在?若存在求出C點的坐標,若不存在,請說明理由. 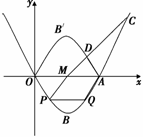
解: (1)方法一:設二次函數的解析式為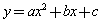
 則
則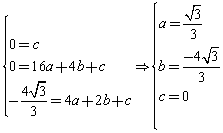
∴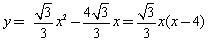
方法二:∵圖像過點O(0,0), A(4,0),
∴設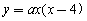 ,
,
又B(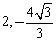 )在曲線上,∴
)在曲線上,∴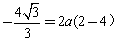 ,∴
,∴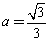
∴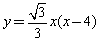
(2)∵M是OA的中點,OA=4,∴MA=2,
若四邊形PQAM是菱形,則PQ=2,
又根據拋物線關于對稱軸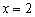 對稱,即P、Q關于直線
對稱,即P、Q關于直線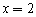 對稱,
對稱,
∴P的橫坐標為1, Q的橫坐標為3.
∴P的坐標為(1, , Q的橫坐標為(3,
, Q的橫坐標為(3, .
.
而計算PM=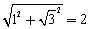 ,故所求的P(1,
,故所求的P(1,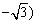 滿足四邊形PQAM是菱形
滿足四邊形PQAM是菱形
(3)設存在這樣的C點.設C、D的坐標分別為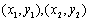
∵二次函數在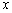 軸下方的部分向上翻折,得曲線OB′A,
軸下方的部分向上翻折,得曲線OB′A,
∴曲線OB′A的解析式為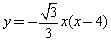
若△CDA的面積是△MDA面積的2倍,
∴△CMA的面積是△MDA面積的3倍,
∴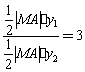 , ∴
, ∴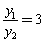 ,即
,即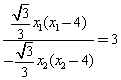 ,
,
∴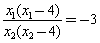 ……………①
……………①
過D,C分別作DD1,CC1垂直于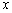 軸,
軸,
∴△MD1D∽△MC1C,
∴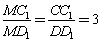 ,∴
,∴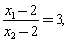
即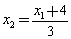 ………………②
………………②
將②代入①得: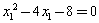
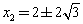 ,代入二次函數的解析式得
,代入二次函數的解析式得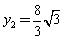
故C的坐標為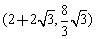 ,或
,或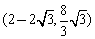 .
.


 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:初中數學 來源: 題型:
某商場銷售的一款空調機每臺的標價是1635元,再一次促銷活動中,按標價的八折銷售,仍可盈利9%.
(1)求這款空調每臺的進價:
(2)在這次促銷活動中,商場銷售了這款空調機100臺,問盈利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
小美周末來到公園,發現在公園一角有一種“守株待兔”游戲.游戲設計者提供了一只兔子和一個有A、B、C、D、E五個出入口的兔籠,而且籠內的兔子從每個出入口走出兔籠的機會是均等的. 規定①玩家只能將小兔從A、B兩個出入口放入,②如果小兔進入籠子后選擇從開始進入的出入口離開,則可獲得一只價值5元小兔玩具,否則應付費3元.
(1)問小美得到小兔玩具的機會有多大?
(2)假設有100人次玩此游戲, 估計游戲設計者可賺多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
環境空氣質量問題已經成為人們日常生活所關心的重要問題。我國新修訂的《環境空氣質量標準》中增加了 監測指標,“
監測指標,“ ”是指大氣中危害健康的直徑小于或等于
”是指大氣中危害健康的直徑小于或等于 微米的顆粒物。
微米的顆粒物。 微米即
微米即 米。用科學記數法表示
米。用科學記數法表示 為【 】
為【 】
A. B.
B. C.
C.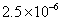 D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
觀察下列等式:
第一個等式:
第二個等式: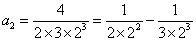
第三個等式: 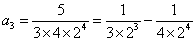
第四個等式:
按上述規律,回答以下問題:
(1) 用含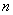 的代數式表示第
的代數式表示第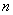 個等式:
個等式: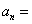
 ;
;
(2) 式子 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com