
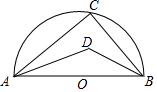
 如圖,AB=4,以AB為直徑作半圓,C為半圓周上一點,D為△ABC內心,△ABD的外接圓半徑為2$\sqrt{2}$.
如圖,AB=4,以AB為直徑作半圓,C為半圓周上一點,D為△ABC內心,△ABD的外接圓半徑為2$\sqrt{2}$. 分析 根據圓周角定理得到∠ACB=90°,根據內心的性質得到∠ADB=135°,根據圓內接四邊形的性質、圓周角定理得到∠AIB=90°,根據等腰直角三角形的性質計算即可.
解答 解:∵AB為半圓的直徑,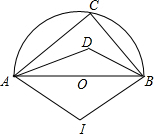
∴∠ACB=90°,
∵D為△ABC內心,
∴∠DAB=$\frac{1}{2}$∠CAB,∠DBA=$\frac{1}{2}$∠CBA,
∴∠ADB=180°-(∠DAB+∠DBA)=180°-45°=135°,
設△ABD的外接圓的圓心為I,
則∠AIB=90°,
∴△ABD的外接圓的半徑為:4×sin45°=2$\sqrt{2}$,
故答案為:2$\sqrt{2}$.
點評 本題考查的是三角形的外接圓和外心、內切圓與內心,掌握圓周角定理、圓內接四邊形的性質、勾股定理是解題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:選擇題
| A. | y=x-1 | B. | y=$\frac{8}{x^2}$ | C. | y=-2x-1 | D. | $\frac{y}{x}$=2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 將拋物線y=x2向左平移4個單位后,再向下平移2個單位,則此時拋物線的解析式是y=(x+4)2-2 | |
| B. | 方程x2+2x+3=0有兩個不相等的實數根 | |
| C. | 平行四邊形既是中心對稱圖形又是軸對稱圖形 | |
| D. | 平分弦的直徑垂直于弦,并且平分這條弦所對的兩條弧 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
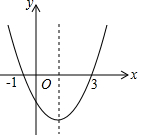 已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則下列6個結論正確的有5個
已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則下列6個結論正確的有5個查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
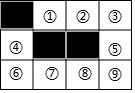 在由相同的小正方形組成的3×4的網格中,有3個小正方形已經涂黑,請你再涂黑一個小正方形,使涂黑的四個小正方形中,其中兩個可以由另外兩個平移得到,則還需要涂黑的小正方形序號是( )
在由相同的小正方形組成的3×4的網格中,有3個小正方形已經涂黑,請你再涂黑一個小正方形,使涂黑的四個小正方形中,其中兩個可以由另外兩個平移得到,則還需要涂黑的小正方形序號是( )| A. | ①或② | B. | ③或④ | C. | ⑤或⑥ | D. | ①或⑨ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com