
如圖1,邊長為4的正方形ABCD中,點E在AB邊上(不與點A,B重合),點F在BC邊上(不與點B,C重合).
第一次操作:將線段EF繞點F順時針旋轉,當點E落在正方形上時,記為點G;
第二次操作:將線段FG繞點G順時針旋轉,當點F落在正方形上時,記為點H;依次操作下去…
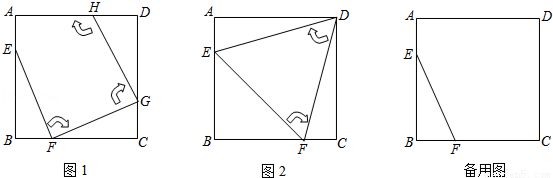
(1)圖2中的△EFD是經過兩次操作后得到的,其形狀為 ,
(2)若經過三次操作可得到四邊形EFGH.
①請判斷四邊形EFGH的形狀為 ,此時AE與BF的數量關系是 ;
②以①中的結論為前提,設AE的長為x,四邊形EFGH的面積為y,求y與x的函數關系式及面積y的取值范圍。
(1)等邊三角形;(2)正方形;AE=BF; =2(x-2)2+8,8≤y<16.
【解析】
試題分析:(1)由旋轉性質,易得△EFD是等邊三角形;利用等邊三角形的性質、勾股定理求出EF的長;
(2)①四邊形EFGH的四邊長都相等,所以是正方形;利用三角形全等證明AE=BF;
②求面積y的表達式,這是一個二次函數,利用二次函數性質求出最值及y的取值范圍.
試題解析:(1)如題圖2,由旋轉性質可知EF=DF=DE,則△DEF為等邊三角形.
在Rt△ADE與Rt△CDF中,
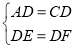
∴Rt△ADE≌Rt△CDF(HL)
∴AE=CF.
設AE=CF=x,則BE=BF=4-x
∴△BEF為等腰直角三角形.
∴EF=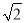 BF=
BF=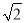 (4-x).
(4-x).
∴DE=DF=EF=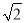 (4-x).
(4-x).
在Rt△ADE中,由勾股定理得:AE2+AD2=DE2,即:x+42=[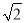 (4-x]2,
(4-x]2,
解得:x1=8-4 ,x2=8+4
,x2=8+4 (舍去)
(舍去)
∴EF=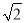 (4-x)=4
(4-x)=4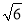 -4
-4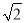 .
.
DEF的形狀為等邊三角形,EF的長為4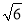 -4
-4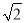 .
.
(2)①四邊形EFGH的形狀為正方形,此時AE=BF.理由如下:
依題意畫出圖形,如答圖1所示:
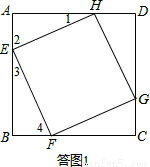
由旋轉性質可知,EF=FG=GH=HE,∴四邊形EFGH的形狀為正方形.
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3.
∵∠3+∠4=90°,∠2+∠3=90°,
∴∠2=∠4.
在△AEH與△BFE中,

∴△AEH≌△BFE(ASA)
∴AE=BF.
②利用①中結論,易證△AEH、△BFE、△CGF、△DHG均為全等三角形,
∴BF=CG=DH=AE=x,AH=BE=CF=DG=4-x.
∴y=S正方形ABCD-4S△AEH=4×4-4×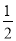 x(4-x)=2x2-8x+16.
x(4-x)=2x2-8x+16.
∴y=2x2-8x+16(0<x<4)
∵y=2x2-8x+16=2(x-2)2+8,
∴當x=2時,y取得最小值8;當x=0時,y=16,
∴y的取值范圍為:8≤y<16.
考點:幾何變換綜合題.


 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:初中數學 來源:2014-2015學年江蘇省鹽城市阜寧縣八年級上學期期中調研數學試卷(解析版) 題型:填空題
如圖,在△ABC中,AB=AC,∠BAC的角平分線交BC邊于點D,AB=5,BC=6,則AD= .

查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省鹽城市阜寧縣八年級上學期期中調研數學試卷(解析版) 題型:選擇題
如圖,在△ABC中,AB=AC,∠A=36°,兩條角平分線BE、CD相交于點O,則圖中全等等腰三角形有
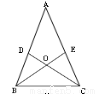
A.1對 B.2對 C.3對 D.4對
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省金華市青春共同體九年級上學期期中考試數學試卷(解析版) 題型:解答題
如圖,某中心廣場燈柱AB被鋼纜CD固定,已知CB=5米,且sin∠DCB=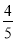 .
.

(1)求鋼纜CD的長度。
(2)若AD=2米,燈的頂端E距離A處1.6米,且∠EAB=120°,則燈的頂端E距離地面多少米?
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省金華市青春共同體九年級上學期期中考試數學試卷(解析版) 題型:填空題
二次函數y=ax2+bx+c的圖象與x軸相交于(-1, 0)和(5, 0)兩點,則該拋物線的對稱軸是 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省濰坊地區九年級上學期期末質量評估數學試卷(解析版) 題型:填空題
在△ABC中,AB=AC=5,tanB=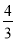 .若⊙O的半徑為
.若⊙O的半徑為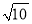 ,且⊙O經過點B、C,那么線段OA的長等于 .
,且⊙O經過點B、C,那么線段OA的長等于 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年甘肅省白銀市會寧縣九年級上學期期末考試數學試卷(解析版) 題型:解答題
如圖,點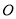 是等邊
是等邊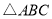 內一點,∠AOB=110°,∠BOC=α.將△BOC繞點C按順時針方向旋轉60°得△ADC,連接OD.
內一點,∠AOB=110°,∠BOC=α.將△BOC繞點C按順時針方向旋轉60°得△ADC,連接OD.

(1)求證:△COD是等邊三角形;
(2)當α=150°時,試判斷△AOD的形狀,并說明理由;
(3)探究:當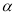 為多少度時,△AOD是等腰三角形?
為多少度時,△AOD是等腰三角形?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com