
分析 (1)根據題意可以求得降價前服裝店每天銷售該服裝可獲的利潤;
(2)根據題意可以列出相應的方程,從而可以求得每件服裝應降的錢數,注意要使顧客得到更多的實惠;
(3)根據題意可以得到利潤與降價的函數關系式,然后化為頂點式,即可解答本題.
解答 解:(1)由題意可得,
降價前服裝店每天銷售該服裝可獲利:(100-60)×20=40×20=800(元),
即降價前服裝店每天銷售該服裝可獲利800元;
(2)設每件服裝降價x元,
(100-60-x)(20+2x)=1200,
解得,x1=10,x2=20,
∵要使顧客得到更多的實惠,
∴每件服裝應降價20元;
(3)設每件服裝降價x元,利潤為W元,
W=(100-60-x)(20+2x)=-2(x-15)2+1250,
∴當x=15時,W取得最大值,此時W=1250,
即每件服裝降價15元服裝店可獲得最大利潤,最大利潤是1250元.
點評 本題考查二次函數的應用,一元二次方程的應用,解答此類問題的關鍵是明確題意,找出所求問題需要的條件,列出相應的方程或函數關系式.


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:初中數學 來源: 題型:選擇題
| A. | 甲班 | B. | 乙班 | C. | 兩班一樣整齊 | D. | 無法確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在菱形ABCD中,對角線AC與BD相交于點O,且AC=6,BD=8,則菱形ABCD的高AH的值是( )
如圖,在菱形ABCD中,對角線AC與BD相交于點O,且AC=6,BD=8,則菱形ABCD的高AH的值是( )| A. | 4 | B. | 5 | C. | $\frac{24}{5}$ | D. | $\frac{48}{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -3和$\sqrt{(-3)^{2}}$ | B. | $\sqrt{(-3)}$和-$\frac{1}{3}$ | C. | -3和$\root{3}{-27}$ | D. | $\root{3}{27}$和|-3| |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
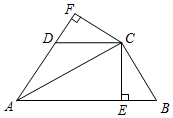 如圖,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,
如圖,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com