
 如圖,△ABC的兩條中線AD、CE交于點G,且AD⊥CE,聯結BG并延長與AC交于點F,如果AD=9,CE=12,那么下列結論不正確的是( )
如圖,△ABC的兩條中線AD、CE交于點G,且AD⊥CE,聯結BG并延長與AC交于點F,如果AD=9,CE=12,那么下列結論不正確的是( )| A. | AC=10 | B. | AB=15 | C. | BG=10 | D. | BF=15 |
分析 根據題意得到點G是△ABC的重心,根據重心的性質得到AG=$\frac{2}{3}$AD=6,CG=$\frac{2}{3}$CE=8,EG=$\frac{1}{3}$CE=4,根據勾股定理求出AC、AE,判斷即可.
解答 解:∵△ABC的兩條中線AD、CE交于點G,
∴點G是△ABC的重心,
∴AG=$\frac{2}{3}$AD=6,CG=$\frac{2}{3}$CE=8,EG=$\frac{1}{3}$CE=4,
∵AD⊥CE,
∴AC=$\sqrt{A{G}^{2}+C{G}^{2}}$=10,A正確;
AE=$\sqrt{A{G}^{2}+E{G}^{2}}$=2$\sqrt{13}$,
∴AB=2AE=4$\sqrt{13}$,B錯誤;
∵AD⊥CE,F是AC的中點,
∴GF=$\frac{1}{2}$AC=5,
∴BG=10,C正確;
BF=15,D正確,
故選:B.
點評 本題考查的是三角形的重心的概念和性質,三角形的重心是三角形三條中線的交點,且重心到頂點的距離是它到對邊中點的距離的2倍.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:初中數學 來源: 題型:填空題
 把編號為1,2,3,4,…的若干盆花按下圖所示擺放,花盆中的花按紅、黃、藍、紫的顏色依次循環排列,則第8行從左邊數第6盆花的顏色為黃色色.
把編號為1,2,3,4,…的若干盆花按下圖所示擺放,花盆中的花按紅、黃、藍、紫的顏色依次循環排列,則第8行從左邊數第6盆花的顏色為黃色色.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
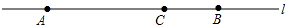 如圖,已知點A、點B是直線上的兩點,AB=12厘米,點C在線段AB上,且AC=8厘米.點P、點Q是直線上的兩個動點,點P的速度為1厘米/秒,點Q的速度為2厘米/秒.點P、Q分別從點C、點B同時出發,在直線上運動,則經過2、10、$\frac{2}{3}$或$\frac{10}{3}$秒時線段PQ的長為6厘米.
如圖,已知點A、點B是直線上的兩點,AB=12厘米,點C在線段AB上,且AC=8厘米.點P、點Q是直線上的兩個動點,點P的速度為1厘米/秒,點Q的速度為2厘米/秒.點P、Q分別從點C、點B同時出發,在直線上運動,則經過2、10、$\frac{2}{3}$或$\frac{10}{3}$秒時線段PQ的長為6厘米.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在正方形ABCD中,△BPC是等邊三角形,BP、CP的延長線分別交AD于點E、F,連結BD、DP,BD與CF相交于點H.給出下列結論:①△BDE∽△DPE;②$\frac{FP}{PH}=\frac{3}{5}$;③DP2=PH•PB;④tan∠DBE=2-$\sqrt{3}$.其中正確結論的序號是①③④.
如圖,在正方形ABCD中,△BPC是等邊三角形,BP、CP的延長線分別交AD于點E、F,連結BD、DP,BD與CF相交于點H.給出下列結論:①△BDE∽△DPE;②$\frac{FP}{PH}=\frac{3}{5}$;③DP2=PH•PB;④tan∠DBE=2-$\sqrt{3}$.其中正確結論的序號是①③④.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com