解:(1)在Rt△EOB中EO=
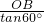
=
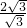
=2,
∴點E的坐標為(-2,0),
在Rt△COA中,OC=OA•tan∠CAO=OA•tan60°=

×

=3,
∴點C的坐標為(-3,0).
(2)∵點C關于對稱軸x=-2對稱的點的坐標為(-1,0),
點C與點(-1,0)都在拋物線上,
設y=a(x+1)(x+3),把A(0,

)代入得,

=a(0+1)(0+3),
∴a=

,
∴y=

(x+1)(x+3)
即y=

x
2+
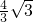
x+

.
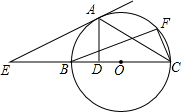
(3)⊙M與⊙A外切,
證明如下:∵ME∥y軸,
∴∠MED=∠B,
∵∠B=∠BDA=∠MDE,
∴∠MED=∠MDE,
∴ME=MD,
∵MA=MD+AD=ME+AD,
∴⊙M與⊙A外切.
分析:(1)已知了A點的坐標,即可得出圓的半徑和直徑,可在直角三角形BOE中,根據∠BEO和OB的長求出OE的長進而可求出E點的坐標,同理可在直角三角形OAC中求出C點的坐標.
(2)已知了對稱軸的解析式,可據此求出C點關于對稱軸對稱的點的坐標,然后根據此點坐標以及C,A的坐標用待定系數法即可求出拋物線的解析式.
(3)兩圓應該外切,由于直線DE∥OB,因此∠MED=∠ABD,由于AB=AD,那么∠ADB=∠ABD,將相等的角進行置換后可得出∠MED=∠MDE,即ME=MD,因此兩圓的圓心距AM=ME+AD即兩圓的半徑和,因此兩圓外切.
點評:本題著重考查了待定系數法求二次函數解析式、切線的性質、圓與圓的位置關系等知識點.

 )為圓心的圓與x軸相切于坐標原點O,與y軸相交于點B,弦BD
)為圓心的圓與x軸相切于坐標原點O,與y軸相交于點B,弦BD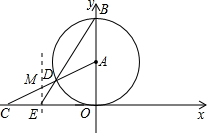 的延長線交x軸的負半軸于點E,且∠BEO=60°,AD的延長線交x軸于點C.
的延長線交x軸的負半軸于點E,且∠BEO=60°,AD的延長線交x軸于點C.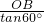 =
=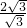 =2,
=2, ×
× =3,
=3, )代入得,
)代入得, =a(0+1)(0+3),
=a(0+1)(0+3), ,
, (x+1)(x+3)
(x+1)(x+3) x2+
x2+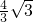 x+
x+ .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 A點運動,E為AB上一動點,點E以1cm/s的速度從A點出發向點B運動.
A點運動,E為AB上一動點,點E以1cm/s的速度從A點出發向點B運動.


 D,過A作AE∥BF交CB的延長線于E.
D,過A作AE∥BF交CB的延長線于E. (2012•張家港市模擬)如圖,以矩形OABC的頂點O為坐標原點,OA所在的直線為x軸,OC所在的直線為y軸,建立直角坐標系.已知OA=3,OC=2,點E是AB的中點,點F在BC上,CF=1,點M、N分別是x軸、y軸上的動點,則四邊形MEFN周長的最小值為
(2012•張家港市模擬)如圖,以矩形OABC的頂點O為坐標原點,OA所在的直線為x軸,OC所在的直線為y軸,建立直角坐標系.已知OA=3,OC=2,點E是AB的中點,點F在BC上,CF=1,點M、N分別是x軸、y軸上的動點,則四邊形MEFN周長的最小值為