
(本小題滿分12分)如圖,在平面直角坐標系中,以點C(1,1)為圓心,2為半徑作圓,交x軸于A,B兩點,開口向下的拋物線經過點A,B,且其頂點P在⊙C上.

(1)求∠ACB的大小;
(2)寫出A,B兩點的坐標;
(3)試確定此拋物線的解析式;
(4)在該拋物線上是否存在一點D,使線段OP與CD互相平分?若存在,求出點D的坐標;若不存在,請說明理由.
(1)120°;(2)A(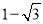 ,0),B(
,0),B(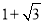 ,0);(3)
,0);(3)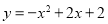 ;(4)D(0,2).
;(4)D(0,2).
【解析】
試題分析:(1)可通過構建直角三角形來求解.過C作CH⊥AB于H,在直角三角形ACH中,根據半徑及C點的坐標即可用三角形函數求出∠ACB的值.
(2)根據垂徑定理可得出AH=BH,然后在直角三角形ACH中可求出AH的長,再根據C點的坐標即可得出A、B兩點的坐標.
(3)根據拋物線和圓的對稱性,即可得出圓心C和P點必在拋物線的對稱軸上,因此可得出P點的坐標為(1,3).然后可用頂點式二次函數通式來設拋物線的解析式.根據A或B的坐標即可確定拋物線的解析式.
(4)如果OP、CD互相平分,那么四邊形OCPD是平行四邊形.因此PC平行且相等于OD,那么D點在y軸上,且坐標為(0,2).然后將D點坐標代入拋物線的解析式中即可判定出是否存在這樣的點.
試題解析:(1)作CH⊥x軸,H為垂足,
∵CH=1,半徑CB=2,∠BCH=60°,∴∠ACB=120°.
(2)∵CH=1,半徑CB=2,∴HB=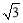 ,故A(
,故A(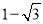 ,0),B(
,0),B(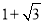 ,0).
,0).
(3)由圓與拋物線的對稱性可知拋物線的頂點P的坐標為(1,3)
設拋物線解析式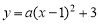 ,把點B(
,把點B(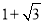 ,0)代入上式,解得
,0)代入上式,解得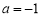 ,∴
,∴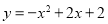 ;
;
(4)假設存在點D使線段OP與CD互相平分,則四邊形OCPD是平行四邊形,∴PC∥OD且PC=OD.
∵PC∥y軸,∴點D在y軸上.
又∵PC=2,∴OD=2,即D(0,2).
又D(0,2)滿足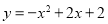 ,∴點D在拋物線上,∴存在D(0,2)使線段OP與CD互相平分.
,∴點D在拋物線上,∴存在D(0,2)使線段OP與CD互相平分.
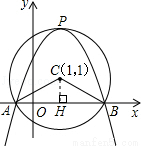
考點:二次函數綜合題.


科目:初中數學 來源:2014-2015學年浙江省聯盟八年級上學期期中數學試卷(解析版) 題型:解答題
如圖(1),邊長為6的等邊三角形ABC中,點D沿射線AB方向由A向B運動,點F同時從C出發,以相同的速度沿射線BC方向運動,過點D作DE⊥AC,連結DF交射線AC于點G.

(1)當點D運動到AB的中點時,求AE的長;
(2)當DF⊥AB時,求AD的長及△BDF的面積;
(3)小明通過測量發現,當點D在線段AB上時,EG的長始終等于AC的一半,他想當點D運動到圖(2)的情況時,EG的長始終等于AC的一半嗎?若改變,說明理由,若不變,請證明EG等于AC的一半.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省杭州地區八年級上學期期中質量檢測數學試卷(解析版) 題型:解答題
(本題10分)如圖甲,已知:在△ABC中,∠BAC=90º,AB=AC,直線m經過點A,BD⊥直線m, CE⊥直線m,垂足分別為點D、E,設BD=m,CE=n.
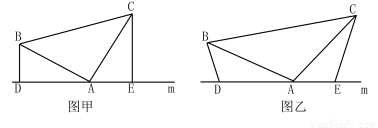
(1)求DE的長(用含m,n的代數式表示);
(2)如圖乙,將(1)中的條件改為:在△ABC中,AB=AC,D、A、E三點都在直線m上,并且有∠BDA=∠AEC=∠BAC= (0º<
(0º< <180º),設BD=m,CE=n.問DE的長如何表示?并請證明你的結論
<180º),設BD=m,CE=n.問DE的長如何表示?并請證明你的結論
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省杭州市聯盟學校九年級上學期期中考試數學試卷(解析版) 題型:選擇題
下列三個命題:
①圓既是軸對稱圖形,又是中心對稱圖形;
②垂直于弦的直徑平分這條弦;
③相等圓心角所對的弧相等;
其中是真命題有( )
A.0個 B.1個 C.2個 D.3個
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省杭州市聯盟學校九年級上學期期中考試數學試卷(解析版) 題型:解答題
(本小題滿分8分)
“中國夢”關乎每個人的幸福生活,為進一步感知我們身邊的幸福,展現成都人追夢的風采,我市某校開展了以“夢想中國,逐夢成都”為主題的攝影大賽,要求參賽學生每人交一件作品.現將參賽的50件作品的成績(單位:分)進行統計如下:

請根據上表提供的信息,解答下列問題:
(1)表中的x的值為 ,y的值為 ;
(2)將本次參賽作品獲得A等級的學生一次用A1,A2,A3,…表示,現該校決定從本次參賽作品中獲得A等級學生中,隨機抽取兩名學生談談他們的參賽體會,請用樹狀圖或列表法求恰好抽到學生A1和A2的概率.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省杭州市蕭山區高橋教育九年級上學期第二次檢測數學試卷(解析版) 題型:選擇題
一個不透明的布袋中裝進A只紅球,B只白球,它們除顏色外無其他差別.吳剛從袋中任意摸出一球,問他摸出的球是紅球的概率為( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省杭州市蕭山區高橋教育九年級上學期第二次檢測數學試卷(解析版) 題型:填空題
假設拋一枚均勻硬幣20次,有8次出現正面,12次出現反面,則你認為拋一枚均勻硬幣出現正面的概率是
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省杭州市蕭山地區九年級上學期期中考試數學試卷(解析版) 題型:填空題
甲、乙兩人玩猜數字游戲,游戲規則如下:有四個數字0、1、2、3,先由甲心中任選一個數字,記為m,再由乙猜甲剛才所選的數字,記為n.若m、n滿足|m-n|≤1,則稱甲、乙兩人“心有靈犀”概率是
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省杭州市蕭山地區九年級上學期期中考試數學試卷(解析版) 題型:選擇題
如圖,二次函數 的圖象在
的圖象在 軸上方的一部分,對于這段圖象與
軸上方的一部分,對于這段圖象與 軸所圍成的陰影部分的面積,你認為與其最接近的值是( )
軸所圍成的陰影部分的面積,你認為與其最接近的值是( )

A.16 B. C.
C. D.32
D.32
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com