
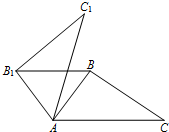
 如圖,在△ABC中,∠BAC=50°,將△ABC繞點A按逆時針方向旋轉(zhuǎn)后得△AB1C1.當B1B∥AC時,求∠BAC1的度數(shù).
如圖,在△ABC中,∠BAC=50°,將△ABC繞點A按逆時針方向旋轉(zhuǎn)后得△AB1C1.當B1B∥AC時,求∠BAC1的度數(shù). 分析 先依據(jù)平行的性質(zhì)可求得∠ABB1的度數(shù),然后再由旋轉(zhuǎn)的性質(zhì)得到△AB1B為等腰三角形,∠B1AC1=50°,再求得∠BAB1的度數(shù),最后依據(jù)∠BAC1=∠BAB1-∠C1AB1求解即可.
解答 解:∵B1B∥AC,
∴∠ABB1=∠BAC=50°.
∵由旋轉(zhuǎn)的性質(zhì)可知:∠B1AC1=∠BAC=50°,AB=AB1.
∴∠ABB1=∠AB1B=50°.
∴∠BAB1=80°
∴∠BAC1=∠BAB1-∠C1AB1=80°-50°=30°.
點評 本題主要考查的是旋轉(zhuǎn)的性質(zhì)、平行線的判斷,求得∠BAB1的度數(shù)是解題的關(guān)鍵.


科目:初中數(shù)學 來源: 題型:選擇題
| A. | 0.25×10-5 | B. | 2.5×10-6 | C. | 25×10-7 | D. | 2.5×106 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
| 銷售時段 | 第一周 | 第二周 | |
| 銷售數(shù)量(臺) | A型 | 5 | 10 |
| B型 | 3 | 5 | |
| 銷售收入(萬元) | 3.98 | 7.4 | |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,在平面直角坐標系中,已知點A(0,2),B(4,0),C(4,3)三點.
如圖,在平面直角坐標系中,已知點A(0,2),B(4,0),C(4,3)三點.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖,將邊長為$\sqrt{3}$cm的正方形ABCD繞點A逆時針方向旋轉(zhuǎn)30°后得到正方形AB′C′D′,則圖中陰影部分的面積為( )
如圖,將邊長為$\sqrt{3}$cm的正方形ABCD繞點A逆時針方向旋轉(zhuǎn)30°后得到正方形AB′C′D′,則圖中陰影部分的面積為( )| A. | $\frac{3}{4}$cm2 | B. | $\frac{3}{2}$cm2 | C. | $\sqrt{3}$cm2 | D. | (3-$\sqrt{3}$)cm2 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 在如圖所示的正方形網(wǎng)格中,每個小正方形的邊長均為1,格點三角形(頂點是網(wǎng)格線的交點的三角形)ABC的頂點A、C的坐標分別為(-4,5)、(-1,3).
在如圖所示的正方形網(wǎng)格中,每個小正方形的邊長均為1,格點三角形(頂點是網(wǎng)格線的交點的三角形)ABC的頂點A、C的坐標分別為(-4,5)、(-1,3).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com