
 如圖,將邊長為$\sqrt{3}$cm的正方形ABCD繞點A逆時針方向旋轉30°后得到正方形AB′C′D′,則圖中陰影部分的面積為( )
如圖,將邊長為$\sqrt{3}$cm的正方形ABCD繞點A逆時針方向旋轉30°后得到正方形AB′C′D′,則圖中陰影部分的面積為( )| A. | $\frac{3}{4}$cm2 | B. | $\frac{3}{2}$cm2 | C. | $\sqrt{3}$cm2 | D. | (3-$\sqrt{3}$)cm2 |
分析 設BC、C′D′相交于點M,連結AM.根據HL即可證明△AD′M≌△ABM,可得到∠MAB=30°,然后可求得MB的長,從而可求得△ABM的面積,最后
利用正方形的面積減去△AD′M和△ABM的面積進行計算即可.
解答 解:設BC、C′D′相交于點M,連結AM.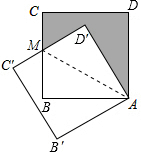
由旋轉的性質可知:AD=AD′.
在直角△AD′M和直角ABM中$\left\{\begin{array}{l}{AD′=AB}\\{AM=AM}\end{array}\right.$,
∴△AD′M≌△ABM.
∴∠BAM=∠D′AM,S△AMB=S△AD′B.
∵∠DAD′=30°,
∴∠MAB=$\frac{1}{2}$×(90°-30°)=30°.
又∵BA=$\sqrt{3}$,
∴MB=$\frac{\sqrt{3}}{3}$AB=1.
∴S△AMB=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
又∵S正方形ABCD=($\sqrt{3}$)2=3,
∴S陰影=3-2×$\frac{\sqrt{3}}{2}$=3-$\sqrt{3}$.
故選:D.
點評 本題考查旋轉的性質以及全等三角形的判定與性質、特殊銳角三角函數值的應用,證得△AD′M≌△ABM是本題的關鍵.


科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,四邊形ABCD是正方形,△ADE旋轉后能與△ABF重合.
如圖,四邊形ABCD是正方形,△ADE旋轉后能與△ABF重合.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
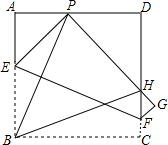 如圖,現有邊長為4的正方形紙片ABCD,點P為AD邊上的一點(不與點A、點D重合),將正方形紙片折疊,使點B落在P處,點C落在G處,PG交DC于H,折痕為EF,連結BP、BH.
如圖,現有邊長為4的正方形紙片ABCD,點P為AD邊上的一點(不與點A、點D重合),將正方形紙片折疊,使點B落在P處,點C落在G處,PG交DC于H,折痕為EF,連結BP、BH.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,四邊形ABCD所在的網格圖中,毎個小正方形的邊長均為1個單位長度.
如圖,四邊形ABCD所在的網格圖中,毎個小正方形的邊長均為1個單位長度.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 電力公司為鼓勵市民節約用電,采取按月用電量分段收費的辦法,已知某戶居民每月應繳電費y(元)與用電量x(度)的函數圖象是一條折線(如圖所示),根據圖象解答下列問題.
電力公司為鼓勵市民節約用電,采取按月用電量分段收費的辦法,已知某戶居民每月應繳電費y(元)與用電量x(度)的函數圖象是一條折線(如圖所示),根據圖象解答下列問題.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com