
 如圖,在直角坐標系中,點A,點B的坐標分別為(2,0),(0,2)
如圖,在直角坐標系中,點A,點B的坐標分別為(2,0),(0,2)分析 (1)先根據A點與B點坐標得到OA=OB=2,根據等腰直角三角形的性質,得到AB=$\sqrt{2}$OA=2$\sqrt{2}$;
(2)由OE⊥OF,根據等角的余角相等得到∠BOE=∠AOF,而OB=OA,OE=OF,得到△BOE≌△AOF,則BE=AF,得到AF+AE=BE+AE=AB=2$\sqrt{2}$;
(3)連MF,△OEF為等腰直角三角形并且OM⊥EF,得到OM為EF的垂直平分線,則MF=ME,又∠OAF=∠OBE=45°,即∠FAM=90°,利用勾股定理得到AM2+AF2=MF2,進行等線段代換后即可得到AM2+BE2=ME2.
解答 解:(1)∵B點坐標為(0,2),A點坐標為(2,0),
∴OB=2,OA=2,
∴△OAB為等腰直角三角形,
∴AB=$\sqrt{2}$OA=2$\sqrt{2}$;
(2)∵OE⊥OF,
∴∠BOE=∠AOF,
在△BOE和△AOF中
$\left\{\begin{array}{l}{OB=OA}\\{∠BOE=∠AOF}\\{OE=OF}\end{array}\right.$,
∴△BOE≌△AOF(SAS),
∴BE=AF,
∴AF+AE=BE+AE=AB=2$\sqrt{2}$;
(3)線段BE、EM、AM的數量關關系為:AM2+BE2=ME2.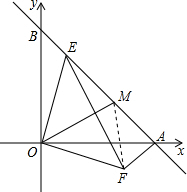
證明:連MF,如圖,∵OE⊥OF,且OE=OF,
∴△OEF為等腰直角三角形,
∵OM⊥EF,
∴OM為EF的垂直平分線,
∴MF=ME,
又∵△BOE≌△AOF,
∴∠OAF=∠OBE=45°,
∴∠FAM=90°,
∴AM2+AF2=MF2,
∴AM2+BE2=ME2.
點評 本題屬于三角形綜合題,主要考查了等腰直角三角形的性質,一次函數的綜合應用,全等三角形的判定與性質、垂直平分線的性質以及勾股定理.解決問題的關鍵是作輔助線構造直角三角形,運用勾股定理得出線段之間的關系式.


 口算題天天練系列答案
口算題天天練系列答案科目:初中數學 來源: 題型:解答題
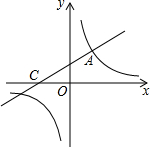 如圖,直線y=$\frac{1}{2}$x+2與雙曲線y=$\frac{k}{x}$相交于點A(m,3),與x軸交于點C.
如圖,直線y=$\frac{1}{2}$x+2與雙曲線y=$\frac{k}{x}$相交于點A(m,3),與x軸交于點C.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 存在三角形使得p=1或p=2 | B. | 0<p<1 | ||
| C. | 1<p<2 | D. | 2<p<3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
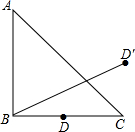 如圖,在△ABC中,AB=BC,∠ABC=90°,D是BC的中點,且它關于AC的對稱點是D′,BD′=$\sqrt{5}$,求AC的長.
如圖,在△ABC中,AB=BC,∠ABC=90°,D是BC的中點,且它關于AC的對稱點是D′,BD′=$\sqrt{5}$,求AC的長.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 兩條直線被第三條直線所截,同位角相等 | |
| B. | 對角線相等的四邊形是矩形 | |
| C. | 兩組對角分別相等的四邊形是平行四邊形 | |
| D. | 在同一個圓中,相等的弦所對的弧相等 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com