Question

17．已知：如圖，AB是⊙O的一條弦，點C為$\widehat{AB}$的中點，CD是⊙O的直徑，過C點的直線l交AB（除端點以外）于點E，交⊙O于點F．
（1）判定圖1中∠CEB與∠FDC的數量關系，并證明你的結論；
（2）將直線l繞C點旋轉（與CD不重合），在旋轉過程中，E點，F點的位置也隨之變化，試在下面備用圖中畫出∠CEB與∠FDC的數量關系發生變化后的圖形，并直接寫出∠CEB與∠FDC的數量關系∠CEB=∠FDC．

Answer 1

分析 （1）根據垂徑定理得到CD⊥AB，∠CFD=90°，然后通過等量代換求證出∠CEB=∠FDC；
（2）根據垂徑定理得到CD⊥AB，∠CFD=90°，然后通過等量代換求證出∠CEB=∠FDC．

解答 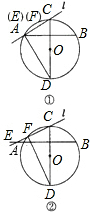（1）解：∠CEB=∠FDC；
理由：∵CD是⊙O的直徑，點C為$\widehat{AB}$的中點，
∴CD⊥AB，
∴∠CEB+∠ECD=90°，
∵CD是⊙O的直徑，
∴∠CFD=90°．
∴∠FDC+∠ECD=90°．
∴∠CEB=∠FDC．

（2）證明：如圖②
∵CD是⊙O的直徑，點C為$\widehat{AB}$的中點，
∴CD⊥AB，
∴∠CEB+∠ECD=90°，
∵CD是⊙O的直徑，
∴∠CFD=90°．
∴∠FDC+∠ECD=90°．
∴∠CEB=∠FDC．
故答案為：∠CEB=∠FDC．

點評 本題考查垂徑定理，圓周角定理，旋轉的性質，正確的作出圖形是解題的關鍵．