
分析 (1)根據等量關系“總利潤=A型號消毒水利潤+B型號消毒水利潤”列出y關于x的函數關系式;
(2)由條件“8天之內完成”“A型號消毒水不得少于1.8萬瓶”確定所獲利潤的最大值即可.
解答 解:(1)設該廠在這次任務中生產A型號消毒水x萬瓶,則生產B型號消毒水(5-x)萬瓶;
y=0.5x+0.3×(5-x)=0.2x+1.5,
由限制條件得:$\left\{\begin{array}{l}{\frac{x}{0.6}+\frac{5-x}{0.8}≤8}\\{1.8≤x≤5}\end{array}\right.$,
解得:1.8≤x≤4.2,
∴自變量x的取值范圍為:1.8≤x≤4.2.
(2)由(1)得y=0.2x+1.5,
∵k=0.2>0,
∴y隨x的增大而增大,
又∵1.8≤x≤4.2,
∴當x=4.2時,y最大總利潤=0.2×4.2+1.5=2.34萬元.
此時生產A型:4.2萬只,B型:0.8萬只.
點評 本題考查了一次函數的應用及一元一次不等式的因應用,需借助函數方程及不等式求解,學生應當注重培養對題理解的能力,解答一次函數的應用問題中,要注意自變量的取值范圍還必須使實際問題有意義.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
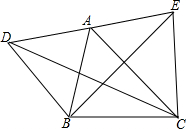 如圖,A為DE的中點,設S1=S△DBC,S2=S△ABC,S3=S△EBC,則S1,S2,S3的關系是( )
如圖,A為DE的中點,設S1=S△DBC,S2=S△ABC,S3=S△EBC,則S1,S2,S3的關系是( )| A. | S2=$\frac{3}{2}$(S1+S3) | B. | S2=$\frac{1}{2}$(S3-S1) | C. | S2=$\frac{1}{2}$(S1+S3) | D. | S2=$\frac{3}{2}$(S3-S1) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com