
 如圖,已知數軸上點A表示的數為a,點B表示的數為b,且滿足(a-6)2+|b+4|=0.
如圖,已知數軸上點A表示的數為a,點B表示的數為b,且滿足(a-6)2+|b+4|=0.分析 (1)根據非負數的性質可得a-6=,b+4=0,計算出a、b的值,然后可計算出AB的長度;
(2)①設點P運動t秒時追上點Q,由題意可得等量關系:點P運動的路程-點Q運動的路程=10,根據等量關系列出方程,再解即可;
②此題要分兩種情況:當P在線段AB之間時;當P在線段AB的延長線上時,分別畫出圖形,根據線段之間的關系進行計算即可.
解答 解:(1)∵(a-6)2+|b+4|=0,
∴a-6=,b+4=0,
解得a=6,b=-4,
∴AB=10,
故答案為:6;-4;10;
(2)①設點P運動t秒時追上點Q,則
6t-4t=10,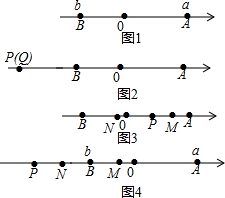
∴t=5,
即:點P運動5秒時追上點Q;
②答:線段MN不發生變化,理由:
當P在線段AB之間時:
MN=AB-(BN+AM),
=AB-($\frac{1}{2}$BP+$\frac{1}{2}$AP)
=AB-$\frac{1}{2}$(BP+AP),
=AB-$\frac{1}{2}$AB=5,
當P在線段AB的延長線上時,
MN=$\frac{1}{2}$AP-$\frac{1}{2}$PB=$\frac{1}{2}$AB=5,
故MN的長不發生變化.
點評 此題主要考查了一元一次方程的應用,非負數的性質,以及線段的和差,關鍵是正確理解題意,考慮全面,畫出圖形.


 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 下列4×4的正方形網格中,小正方形的邊長均為1,三角形的頂點都在格點上,請在圖(1)中畫出一個格點三角形,使它與圖(1)中的△ABC相似.
下列4×4的正方形網格中,小正方形的邊長均為1,三角形的頂點都在格點上,請在圖(1)中畫出一個格點三角形,使它與圖(1)中的△ABC相似.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在△ABC中,點D、E分別在AB、AC上,DE∥BC.若AD=6,DB=3,則$\frac{AE}{AC}$的值為$\frac{2}{3}$.
如圖,在△ABC中,點D、E分別在AB、AC上,DE∥BC.若AD=6,DB=3,則$\frac{AE}{AC}$的值為$\frac{2}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
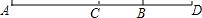 如圖,C為線段AD上一點,B為CD的中點,AD=12cm,BD=3cm.
如圖,C為線段AD上一點,B為CD的中點,AD=12cm,BD=3cm.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x3y4與x3z4 | B. | -3x與-x | C. | 5ab與-2ab | D. | -3x2y與$\frac{1}{2}x$2y |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com