
已知正比例函數y=kx與反比例函數y=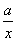 相交于點A(1,b)、點B(c,-2),求k+a的值。甲同學說:未知數太多,很難求的;乙同學說:可能不是用待定系數法來求;丙說:如果用數形結合的方法,利用兩交點在坐標系中位置的特殊性,可以試試。請結合他們的討論求出k+a=________.
相交于點A(1,b)、點B(c,-2),求k+a的值。甲同學說:未知數太多,很難求的;乙同學說:可能不是用待定系數法來求;丙說:如果用數形結合的方法,利用兩交點在坐標系中位置的特殊性,可以試試。請結合他們的討論求出k+a=________.
科目:初中數學 來源: 題型:
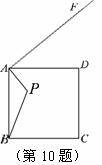
已知點P是邊長為5的正方形ABCD內一點,且AP=2 , AF⊥AP,垂足是點A, 若在射線AF上找一點M,使以點A, M, D為頂點的三角形與△ABP相似,則AM為( )
A. 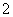 B.
B. 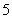 C.
C. 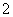 或
或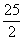 D.
D. 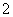 或
或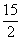
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
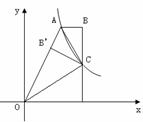
如圖,雙曲線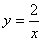 (x>0)經過四邊形OABC的頂點A、C,∠ABC=90°,OC平分OA與
(x>0)經過四邊形OABC的頂點A、C,∠ABC=90°,OC平分OA與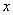 軸正半軸的夾角,AB∥
軸正半軸的夾角,AB∥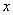 軸,將△ABC沿AC翻折后得到△AB'C,B'點落在OA上,則四邊形OABC的面積是( ).
軸,將△ABC沿AC翻折后得到△AB'C,B'點落在OA上,則四邊形OABC的面積是( ).
A.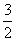 B.
B.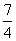 C.2 D.
C.2 D.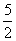
| |
查看答案和解析>>
科目:初中數學 來源: 題型:
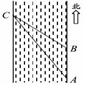
如圖所示,某學生在河東岸點A處觀測到河對岸水邊有一點C,測得C在A北偏西31°的方向上,沿河岸向北前行40米到達B處,測得C在B北偏西45°的方向上,請你根據以上數據,求這條河的寬度.(參考數值:tan31°≈
 )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
某商場銷售甲、乙兩種品牌的智能手機,這兩種手機的進價和售價如下表所示:
| 甲 | 乙 | |
| 進價(元/部) | 4000 | 2500 |
| 售價(元/部) | 4300 | 3000 |
該商場計劃購進兩種手機若干部,共需15.5萬元,預計 全部銷售后獲毛利潤共2.1萬元(毛利潤=(售價-進價)×銷售量)
全部銷售后獲毛利潤共2.1萬元(毛利潤=(售價-進價)×銷售量)
(1)該商場計劃購進甲、乙兩種手機各多少部?
(2)通過市場調研,該商場決定在原計劃的基礎上,減少甲種手機的購進數量,增加乙種手機的購進數量,已知乙種手機增加的數量是甲種手機減少 的數量的3倍,而且用于購進這兩種手機的總資金不超過17.25萬元,該商場怎樣進貨,使全部銷售后獲得的毛利潤最大?并求出最大毛利潤。
的數量的3倍,而且用于購進這兩種手機的總資金不超過17.25萬元,該商場怎樣進貨,使全部銷售后獲得的毛利潤最大?并求出最大毛利潤。
查看答案和解析>>
科目:初中數學 來源: 題型:
在平面直角坐標系中,有反比例函數y = 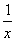 與y = -
與y = - 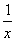 的圖象和正方形ABCD,原點O 與對角線AC、BD的交點重疊,且如圖所示的陰影部分面積為8,則AB= .
的圖象和正方形ABCD,原點O 與對角線AC、BD的交點重疊,且如圖所示的陰影部分面積為8,則AB= .

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com