
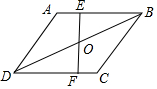
 如圖,在菱形ABCD中,∠C=120°,FE⊥AB于點E,并交BD于點O,恰好O是BD的中點,若AD=6,則四邊形AEFD的周長為( )
如圖,在菱形ABCD中,∠C=120°,FE⊥AB于點E,并交BD于點O,恰好O是BD的中點,若AD=6,則四邊形AEFD的周長為( )| A. | 12+$\frac{3}{2}$$\sqrt{3}$ | B. | 12+3$\sqrt{3}$ | C. | 15 | D. | 18 |
分析 直接利用菱形的性質結合直角三角形的性質得出AN的長,再利用全等三角形的判定與性質得出BE=DF,進而得出答案.
解答  解:過點A作AN⊥DC于點N,
解:過點A作AN⊥DC于點N,
∵四邊形ABCD是菱形,
∴AD=DC=BC=AB=6,
∵∠C=120°,
∴∠ADC=60°,
∴DN=3,
則AN=3$\sqrt{3}$,
∵FE⊥AB,
故可得EF=3$\sqrt{3}$,
∵四邊形ABCD是菱形,
∴AB∥DC,
∴∠EBO=∠CDO,
在△BOE和△DOF中,
$\left\{\begin{array}{l}{∠EBO=∠ODC}\\{BO=DO}\\{∠EOB=∠DOF}\end{array}\right.$,
∴△BOE≌△DOF(ASA),
∴BE=DF,
∴四邊形AEFD的周長為:AE+EF+DF+AD=AD+AB+EF=12+3$\sqrt{3}$.
故選:B.
點評 此題主要考查了菱形的性質以及全等三角形的判定與性質,正確得出△BOE≌△DOF是解題關鍵.


 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:初中數學 來源: 題型:選擇題
| 月使用費(元) | 主叫限定時間(分鐘) | 主叫超時費/(元/分) | 被叫 | |
| 方式一 | 58 | 150 | 0.25 | 免費 |
| 方式二 | 88 | 350 | 0.19 | 免費 |
| A. | 方式一 | B. | 方式二 | C. | 兩種方式一樣 | D. | 無法確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| -0.8 | +1 | -1.2 | -0.1 | -0.6 | +0.6 | -0.3 | -0.2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
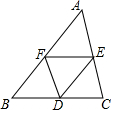 如圖,D、E、F是△ABC三邊的中點,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )
如圖,D、E、F是△ABC三邊的中點,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )| A. | △BDF | B. | △DEF | C. | △CDE | D. | △BDF和△CDE |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在等腰△ABC中,AB=AC,點D,E分別是BC,AB邊的中點,過A點作AF∥BC交DE的延長線于F點,連接AD,BF.
如圖,在等腰△ABC中,AB=AC,點D,E分別是BC,AB邊的中點,過A點作AF∥BC交DE的延長線于F點,連接AD,BF.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com