
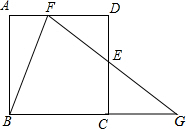
 如圖,在正方形ABCD中,E是CD的中點,F是AD的一個三等分點,設BC的延長線與FE的延長線相交于G.問BF是否平分∠AFG?請說明理由.
如圖,在正方形ABCD中,E是CD的中點,F是AD的一個三等分點,設BC的延長線與FE的延長線相交于G.問BF是否平分∠AFG?請說明理由. 分析 結論:BF平分∠AFG作FH⊥BC于H,則四邊形CDFH是矩形,HF=CD,DF=CH,設正方形的邊長為6a.通過計算證明GF=GB即可解決問題.
解答 解:結論:BF平分∠AFG.
理由:如圖,作FH⊥BC于H,則四邊形CDFH是矩形,HF=CD,DF=CH,設正方形的邊長為6a.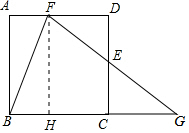
∵F是AD的一個三等分點,
∴AF=2a,DF=HC=4a,FH=CD=6a,
在△DFE和△CGE中,
$\left\{\begin{array}{l}{∠D=∠GCE}\\{DE=EC}\\{∠DEF=∠CEG}\end{array}\right.$,
∴△DFE≌△CGE,
∴CG=DF=4a,
∴GH=8a,
在Rt△FHG中,FG=$\sqrt{F{H}^{2}+G{H}^{2}}$=$\sqrt{(6a)^{2}+(8a)^{2}}$=10a,
∵BG=10a,
∴GF=GB=10a,
∴∠GFB=∠GBF,
∵AD∥BC,
∴∠AFB=∠GBF,
∴∠BFA=∠BFG,
∴BF平分∠AFG.
點評 本題考查正方形的性質、等腰三角形的判定和性質、平行線的性質、勾股定理等知識,解題的關鍵是學會添加常用輔助線,構造直角三角形解決問題,本題體現了數形結合的思想,屬于中考常考題型.


 智慧小復習系列答案
智慧小復習系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,將長方形ABCD沿AE折疊,使點D落在BC邊上的點F,若∠BAF=60°,則∠DAE=( )
如圖,將長方形ABCD沿AE折疊,使點D落在BC邊上的點F,若∠BAF=60°,則∠DAE=( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com