
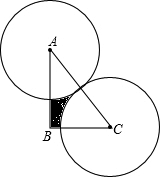
 如圖,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,分別以A、C為圓心,以$\frac{AC}{2}$的長為半徑作圓,將Rt△ABC截去兩個(gè)扇形,則剩余(陰影)部分的面積為6-$\frac{25}{16}$πcm2(結(jié)果保留π)
如圖,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,分別以A、C為圓心,以$\frac{AC}{2}$的長為半徑作圓,將Rt△ABC截去兩個(gè)扇形,則剩余(陰影)部分的面積為6-$\frac{25}{16}$πcm2(結(jié)果保留π) 分析 利用勾股定理得出AB的長,再利用圖中陰影部分的面積是:S△ABC-S扇形面積求出即可.
解答 解:∵Rt△ABC中,∠ABC=90°,AB=4,BC=3,
∴AC=$\sqrt{{4}^{2}+{3}^{2}}$=5(cm),
∴S陰影部分=$\frac{1}{2}$×3×4-$\frac{90π×(\frac{5}{2})^{2}}{360}$=6-$\frac{25}{16}$π(cm2).
故答案是:6-$\frac{25}{16}$π.
點(diǎn)評 本題考查了扇形的面積公式,陰影部分的面積可以看作是直角三角形ABC的面積減去兩個(gè)扇形的面積,求不規(guī)則的圖形的面積,可以轉(zhuǎn)化為幾個(gè)規(guī)則圖形的面積的和或差來求.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,某校要在長為32m,寬為20m的長方形操場上修筑寬度相同的道路(圖中陰影部分),在余下的空白部分種上草坪,要使草坪的面積為540m2,求道路的寬.
如圖,某校要在長為32m,寬為20m的長方形操場上修筑寬度相同的道路(圖中陰影部分),在余下的空白部分種上草坪,要使草坪的面積為540m2,求道路的寬.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
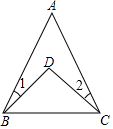 如圖,∠1=15°,∠2=20°,∠A=40°,則∠BDC的度數(shù)為( )
如圖,∠1=15°,∠2=20°,∠A=40°,則∠BDC的度數(shù)為( )| A. | 75° | B. | 95° | C. | 105° | D. | 115° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3(x2-4y2) | B. | 3(x+2y)(x-2y) | C. | 3(2x+y)(2x-y) | D. | 3(x-2y)2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | y=2+0.5x | B. | y=2+x | C. | y=2+2x | D. | y=2x |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,拋物線y=-$\frac{1}{4}$x2+$\frac{9}{4}$與直線y=-$\frac{1}{2}$x+$\frac{3}{2}$交于點(diǎn)A,C的兩點(diǎn),點(diǎn)B是點(diǎn)A關(guān)于y軸的對稱點(diǎn).
如圖,拋物線y=-$\frac{1}{4}$x2+$\frac{9}{4}$與直線y=-$\frac{1}{2}$x+$\frac{3}{2}$交于點(diǎn)A,C的兩點(diǎn),點(diǎn)B是點(diǎn)A關(guān)于y軸的對稱點(diǎn).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
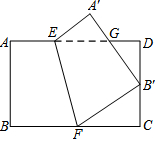 將矩形ABCD沿EF折疊,使點(diǎn)B與CD邊中點(diǎn)B′重合,A′B′交AD于點(diǎn)G,若AE=1,AB=2,BC=3,下面有4個(gè)結(jié)論中,正確的個(gè)數(shù)是( )
將矩形ABCD沿EF折疊,使點(diǎn)B與CD邊中點(diǎn)B′重合,A′B′交AD于點(diǎn)G,若AE=1,AB=2,BC=3,下面有4個(gè)結(jié)論中,正確的個(gè)數(shù)是( )| A. | 1個(gè) | B. | 2個(gè) | C. | 3個(gè) | D. | 4個(gè) |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com