
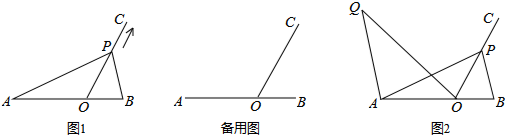
分析 (1)作PH⊥AB于H,根據運動時間和速度求出OP的長,根據正弦的概念求出PH,根據三角形的面積公式計算即可;
(2)分∠ABP=90°和∠APB=90°兩種情況根據相似三角形的性質計算即可;
(3)根據題意補全圖形,根據平行線的性質和等腰三角形的性質證明△QAO∽△OEP,得到AQ•EP=EO•AO,證明△OBE∽△ABP,根據相似三角形的性質解答即可.
解答 解:(1)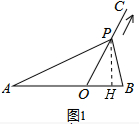 作PH⊥AB于H,
作PH⊥AB于H,
∵動點P以每秒2個單位長度的速度從點O出發,
∴當t=$\frac{1}{2}$秒時,則OP=1,
∵∠BOC=60°,OP=1,
∴PH=OP×sin60°=$\frac{\sqrt{3}}{2}$,
∴S△ABP=$\frac{1}{2}$×AB×PH=$\frac{3\sqrt{3}}{4}$,
故答案為:1;$\frac{3\sqrt{3}}{4}$;
(2)①∵∠A<∠BOC=60°,
∴∠A不可能是直角.
②如備用圖,當∠ABP=90°時,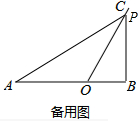
∵∠BOC=60°,
∴∠OPB=30°.
∴OP=2OB,即2t=2.
∴t=1;
③當∠APB=90°,如圖1,
OP=2t,OH=t,PH=$\sqrt{3}$t,AH=2+t,HB=1-t,
∵∠APH+∠BPH=90°,∠B+∠BPH=90°,
∴∠APH=∠B.
∴△APH∽△PBH.
∴$\frac{AH}{PH}$=$\frac{PH}{BH}$,即$\frac{2+t}{\sqrt{3}t}$=$\frac{\sqrt{3}t}{1-t}$,
整理得4t2+t-2=0,
解得t1=$\frac{-1+\sqrt{33}}{8}$,t2=$\frac{-1-\sqrt{33}}{8}$(舍去);
(3)補全圖形,如圖,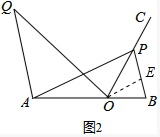
∵AP=AB,
∴∠APB=∠B.
∵OE∥AP,
∴∠OEB=∠APB=∠B.
∵AQ∥BP,
∴∠QAB+∠B=180°.
∵∠OEP+∠OEB=180°,
∴∠OEP=∠QAB.
又∵∠AOC=∠OPB+∠B=∠AOQ+∠QOP,
∵∠B=∠QOP,
∴∠AOQ=∠OPB.
∴△QAO∽△OEP.
∴$\frac{AQ}{EO}$=$\frac{AO}{EP}$,即AQ•EP=EO•AO.
∵OE∥AP,
∴△OBE∽△ABP.
∴$\frac{OE}{AP}$=$\frac{BE}{BP}$=$\frac{BO}{BA}$=$\frac{1}{3}$.
∴OE=$\frac{1}{3}$AP=1,BP=$\frac{3}{2}$EP.
∴AQ•BP=AQ•$\frac{3}{2}$EP=$\frac{3}{2}$AO•OE=$\frac{3}{2}$×2×1=3.
點評 本題考查的是相似三角形的判定和性質、直角三角形的性質,正確作出輔助線、掌握相關定理是解題的關鍵,注意分情況討論思想的應用和解一元二次方程的一般步驟的熟練掌握.


 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:初中數學 來源: 題型:解答題
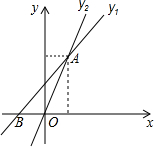 如圖,已知一次函數y1=(m-2)x+2與正比例函數y2=2x圖象相交于點A(2,n),一次函數y1=(m-2)x+2與x軸交于點B.
如圖,已知一次函數y1=(m-2)x+2與正比例函數y2=2x圖象相交于點A(2,n),一次函數y1=(m-2)x+2與x軸交于點B.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
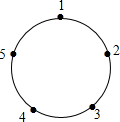 如圖,一只青蛙在圓周上標有數字的五個點上跳,若它停在奇數點上,則下列沿順時針方向跳兩個點:若停在偶數點上,則下次沿逆時針方向跳一個點,若青蛙從1這點開始跳,則經過2016次后它停在哪個數對應的點上( )
如圖,一只青蛙在圓周上標有數字的五個點上跳,若它停在奇數點上,則下列沿順時針方向跳兩個點:若停在偶數點上,則下次沿逆時針方向跳一個點,若青蛙從1這點開始跳,則經過2016次后它停在哪個數對應的點上( )| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com