
| A. | 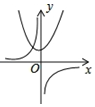 | B. | 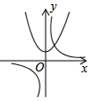 | C. | 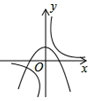 | D. | 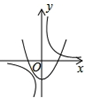 |
分析 先根據各選項中拋物線的位置確定a、b的符號,再根據a、b的符號對雙曲線的大致位置進行判斷即可.
解答 解:A、根據拋物線開口向上,與y軸交于正半軸可得a>0,b>0,即ab>0,所以雙曲線在第一、三象限,故A選項錯誤;
B、根據拋物線開口向上,與y軸交于正半軸可得a>0,b>0,即ab>0,所以雙曲線在第一、三象限,故B選項正確;
C、根據拋物線開口向下,與y軸交于正半軸可得a<0,b>0,即ab<0,所以雙曲線在第二、四象限,故C選項錯誤;
D、根據拋物線開口向上,與y軸交于負半軸可得a>0,b<0,即ab<0,所以雙曲線在第二、四象限,故D選項錯誤.
故選:B.
點評 本題考查了反比例函數圖象以及二次函數的圖象,二次函數y=ax2+bx+c(a、b、c為常數,a≠0)的圖象為拋物線,當a>0,拋物線開口向上;當a<0,拋物線開口向下,與y軸的交點坐標為(0,c).解題時注意:當k>0,雙曲線的兩支分別位于第一、第三象限,在每一象限內y隨x的增大而減小;當k<0,雙曲線的兩支分別位于第二、第四象限,在每一象限內y隨x的增大而增大.


 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{4x}{40}$+$\frac{x+2}{40}$×12=1 | B. | $\frac{4x}{40}$+$\frac{x+2}{40}$×8=1 | ||
| C. | $\frac{12x}{40}+\frac{x+2}{40}$×12=1 | D. | $\frac{12x}{40}+\frac{x+2}{40}$×8=1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在平面直角坐標系中,點A(0,6),B(8,0),AB=10,如圖作∠DBO=∠ABO,∠CAy=∠BAO,直線CD過點O.
在平面直角坐標系中,點A(0,6),B(8,0),AB=10,如圖作∠DBO=∠ABO,∠CAy=∠BAO,直線CD過點O.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com