
分析 如圖,過A作AC⊥x軸于C,過B作BD⊥x軸于D,根據(jù)已知條件得到S△BOD=2,S△ACO=$\frac{1}{2}$,y1=$\frac{1}{{x}_{1}}$y2=$\frac{4}{{x}_{2}}$,于是得到S△AOB=S四邊形ABDC-S△BOD-S△AOC=$\frac{1}{2}$($\frac{4{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$)=$\frac{1}{2}$×$\frac{4{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{x}_{1}{x}_{2}}$≥$\frac{1}{2}$×$\frac{4{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$,于是得到結(jié)論.
解答 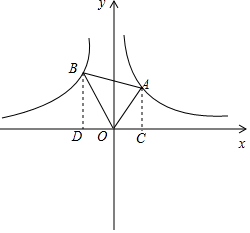 解:如圖,過A作AC⊥x軸于C,過B作BD⊥x軸于D,
解:如圖,過A作AC⊥x軸于C,過B作BD⊥x軸于D,
∵A(x1,y1)是反比例函數(shù)y=$\frac{1}{x}$(x>0)的圖象上的一點(diǎn),B(x2,y2)是反比例函數(shù)y=-$\frac{4}{x}$(x<0)的圖象上的一點(diǎn),
∴S△BOD=2,S△ACO=$\frac{1}{2}$,y1=$\frac{1}{{x}_{1}}$y2=$\frac{4}{{x}_{2}}$,
∴S△AOB=S四邊形ABDC-S△BOD-S△AOC
=$\frac{1}{2}$(y1+y2)(x1+x2)-$\frac{1}{2}$-2
=$\frac{1}{2}$(x1y1+x2y2+x1y2+x2y1)-$\frac{1}{2}$-2
=$\frac{1}{2}$+2+$\frac{1}{2}$(x1y2+x2y1)-$\frac{1}{2}$-2
=$\frac{1}{2}$($\frac{4{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$)
=$\frac{1}{2}$×$\frac{4{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{x}_{1}{x}_{2}}$≥$\frac{1}{2}$×$\frac{4{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$,
即△AOB的面積的最小值為2,
故答案為:2.
點(diǎn)評(píng) 本題考查了反比例函數(shù)系數(shù)k的幾何意義,反比例函數(shù)圖象上點(diǎn)的坐標(biāo)特征,三角形面積的計(jì)算,熟練掌握反比例函數(shù)系數(shù)k的幾何意義是解題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
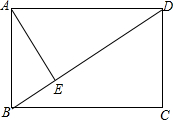 已知:如圖,矩形ABCD,AB長6cm,對(duì)角線BD比AD邊大2cm,則AD的長為8cm,點(diǎn)A到BD的距離AE的長為4.8cm.
已知:如圖,矩形ABCD,AB長6cm,對(duì)角線BD比AD邊大2cm,則AD的長為8cm,點(diǎn)A到BD的距離AE的長為4.8cm.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
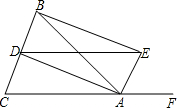 如圖,在△ABC中,AB=AC,AD、AE分別是∠BAC和∠BAF的平分線,BE⊥AE
如圖,在△ABC中,AB=AC,AD、AE分別是∠BAC和∠BAF的平分線,BE⊥AE查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com