
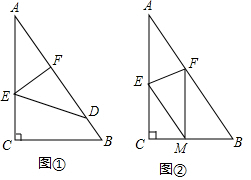
分析 (1)首先證明△AEF∽△ABC,可得$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=($\frac{AE}{AB}$)2=($\frac{2.5}{\sqrt{{3}^{2}+{4}^{2}}}$)2=$\frac{1}{4}$,由此即可解決問題.
(2)①只要證明AE=EM=MF=AF即可.
②設AE=x,則EM=x,CE=4-x,由四邊形AEMF為菱形,推出EM∥AB,推出△CEM∽△CAB,可得$\frac{CE}{CA}$=$\frac{EM}{AB}$,即$\frac{4-x}{4}$=$\frac{x}{5}$,求出x的值,再利用勾股定理即可解決問題.
解答 解:(1)如圖1中,由折疊可知,EF⊥AB,△AEF≌△DEF,
∴∠AFE=∠ACB=90°,
∵∠A=∠A,
∴△AEF∽△ABC,
∴$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=($\frac{AE}{AB}$)2=($\frac{2.5}{\sqrt{{3}^{2}+{4}^{2}}}$)2=$\frac{1}{4}$,
∴S△AEF=$\frac{1}{4}$×$\frac{1}{2}$×3×4=$\frac{3}{2}$.
(2)如圖2中,①由折疊可知,AE=EM,AF=FM,∠AFE=∠MFE,
∵MF∥CA,
∴∠AEF=∠MFE,
∴∠AEF=∠AFE,
∴AE=AF,
∴AE=EM=MF=AF,
∴四邊形AEMF是菱形.
②設AE=x,則EM=x,CE=4-x,
∵四邊形AEMF為菱形,
∴EM∥AB,
∴△CEM∽△CAB,
∴$\frac{CE}{CA}$=$\frac{EM}{AB}$,即$\frac{4-x}{4}$=$\frac{x}{5}$,解得x=$\frac{20}{9}$,
∴AE=EM=$\frac{20}{9}$,CE=$\frac{16}{9}$,
∴CM=$\sqrt{(\frac{20}{9})^{2}-(\frac{16}{9})^{2}}$=$\frac{4}{3}$.
點評 本題考查四邊形綜合題、相似三角形的判定和性質、勾股定理、菱形的判定和性質等知識,解題的關鍵是靈活運用所學知識解決問題,學會利用此時構建方程解決問題,屬于中考常考題型.


科目:初中數學 來源: 題型:選擇題
| A. | -1 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | π | B. | 1 | C. | $\frac{2}{3}$π | D. | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
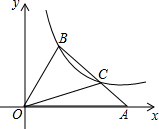 如圖,在平面直角坐標系xOy中,△OAB的頂點A在x軸正半軸上,OC是△OAB的中線,點B、C在反比例函數y=$\frac{k}{x}$(x>0)的圖象上,若△OAB的面積等于6,則k的值為( )
如圖,在平面直角坐標系xOy中,△OAB的頂點A在x軸正半軸上,OC是△OAB的中線,點B、C在反比例函數y=$\frac{k}{x}$(x>0)的圖象上,若△OAB的面積等于6,則k的值為( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com