
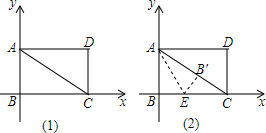
分析 (1)由題意可知:C(4,0)、A(0,3).設AC的解析式為y=kx+b,將點A、C的坐標代入得到關于k、b的二元一次方程組,從而可求得k、b的值,于是可得到直線AC的解析式為y=-$\frac{3}{4}$x+3;
(2)在Rt△ABC中,由勾股定理可求得AC=5,由翻折的性質可知:∠EB′C=90°,BE=BE′,B′C=2,設BE=B′E=x,然后在Rt△B′EC中,由勾股定理列出關于關于x的方程,從而可求得BE=$\frac{3}{2}$;
(3)①如圖(1)所示:過點P作PF⊥AD,垂足為F.由S△ADP=2S△ABE,可求得PF=$\frac{9}{4}$,從而得到點P的縱坐標Py=4-$\frac{9}{4}$=$\frac{7}{4}$,將y=$\frac{7}{4}$代入y=-$\frac{3}{4}$x+3可求得x=$\frac{5}{3}$,從而得到點P的坐標為($\frac{5}{3}$,$\frac{7}{4}$);
②如圖(2)所示:過點P作PF⊥AD,垂足為F.由①可知:PF=$\frac{9}{4}$.可求得點P的縱坐標Py=$\frac{25}{4}$.將y=$\frac{25}{4}$代入y=-$\frac{3}{4}$x+3可求得x=-$\frac{13}{3}$,于是得到點P的坐標為(-$\frac{13}{3}$,$\frac{25}{4}$).
解答 解:(1)∵BC=4,AB=3,
∴C(4,0)、A(0,3).
設AC的解析式為y=kx+b,將點A、C的坐標代入得:$\left\{\begin{array}{l}{4k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=3}\end{array}\right.$.
則直線AC的解析式為y=-$\frac{3}{4}$x+3.
(2)在Rt△ABC中,由勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5.
∵由翻折的性質可知:BE=B′E,AB=AB′=3,∠B=∠AB′E=90°
∴B′C=5-3=2,∠EB′C=90°.
設BE=B′E=x,則EC=4-x.
在Rt△B′EC中,由勾股定理得:EC2=EB′2+B′C2,即(4-x)2=x2+22.
解得:x=$\frac{3}{2}$.
∴BE=$\frac{3}{2}$.
∴點E的坐標為($\frac{3}{2}$,0).
(3)①如圖(1)所示:過點P作PF⊥AD,垂足為F.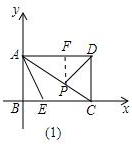
${S}_{△ABE}=\frac{1}{2}AB•BE$=$\frac{1}{2}×3×\frac{3}{2}$=$\frac{9}{4}$.
∵S△ADP=2S△ABE,
∴S△ADP=2×$\frac{9}{4}$=$\frac{9}{2}$.
∴$\frac{1}{2}×AD•PF=\frac{9}{2}$,即$\frac{1}{2}×4×PF=\frac{9}{2}$.
解得:PF=$\frac{9}{4}$.
∴點P的縱坐標Py=4-$\frac{9}{4}$=$\frac{7}{4}$.
將y=$\frac{7}{4}$代入y=-$\frac{3}{4}$x+3得:$-\frac{3}{4}x+3=\frac{7}{4}$.
解得:x=$\frac{5}{3}$.
∴點P的坐標為($\frac{5}{3}$,$\frac{7}{4}$).
②如圖(2)所示:過點P作PF⊥AD,垂足為F.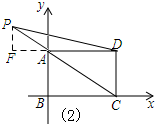
∵由①可知:PF=$\frac{9}{4}$.
∴點P的縱坐標Py=$\frac{9}{4}+4$=$\frac{25}{4}$.
將y=$\frac{25}{4}$代入y=-$\frac{3}{4}$x+3得:-$\frac{3}{4}$x+3=$\frac{25}{4}$.
解得:x=-$\frac{13}{3}$.
∴點P的坐標為(-$\frac{13}{3}$,$\frac{25}{4}$).
綜上所述,點P的坐標為($\frac{5}{3}$,$\frac{7}{4}$)或(-$\frac{13}{3}$,$\frac{25}{4}$).
點評 本題主要考查的是一次函數的綜合應用,解答本題主要應用了待定系數法求一次函數的解析式、勾股定理、三角形的面積公式、一次函數圖象上點的坐標特點,根據點P在線段AC上、在P在線段AC外分類畫出圖形是解題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
 在美化校園的活動中,某興趣小組想借助如圖6所示的直角墻角(CD邊所在的墻長10米,DA邊所在的墻足夠長),用28米長的籬笆圍成一個矩形花園ABCD(籬笆只圍AB,BC兩邊),設AB=x米.
在美化校園的活動中,某興趣小組想借助如圖6所示的直角墻角(CD邊所在的墻長10米,DA邊所在的墻足夠長),用28米長的籬笆圍成一個矩形花園ABCD(籬笆只圍AB,BC兩邊),設AB=x米.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
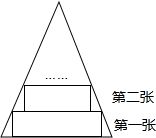 如圖所示,一張等腰三角形紙片,底邊長18cm,底邊上的高長18cm,現沿底邊依次向下往上裁剪寬度均為3cm的矩形紙條,已知剪得的紙條中有一張是正方形,則這張正方形紙條是( )
如圖所示,一張等腰三角形紙片,底邊長18cm,底邊上的高長18cm,現沿底邊依次向下往上裁剪寬度均為3cm的矩形紙條,已知剪得的紙條中有一張是正方形,則這張正方形紙條是( )| A. | 第4張 | B. | 第5張 | C. | 第6張 | D. | 第7張 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com