
【題目】在△ABC中,AB=BC=![]() ,∠ABC=120°,△CDE為等邊三角形,CD=2,連接AD,M為AD中點
,∠ABC=120°,△CDE為等邊三角形,CD=2,連接AD,M為AD中點
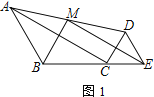
(1)如圖1,當B、C、E三點共線時,證明: BM⊥ME
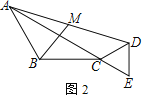
(2)如圖2,當A、C、E三點共線時,求BM的長
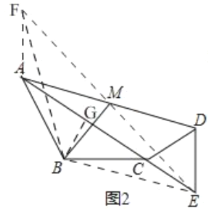
(3)如圖3,取BE中點N,連MN.將△CDE繞點C旋轉,直接寫出旋轉過程中線段MN的取值范圍

【答案】(1)見解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先作出圖形,進而證明△AMF≌△DME,即可得出結論;
(2)同(1)的方法證出△AMF≌△DMF,利用四邊形的內角和定理以及平角的定義得出∠BCE=∠BAF即可得出∠BME=90°,最后利用勾股定理即可得出結論;
(2)同(2)的方法得出∠BME=90°,進而得出BE=2MN,最后利用三角形的三邊關系即可得出結論.
(1)證明:如圖1,延長BA,EM交于點F,即:△FAM即為所求,
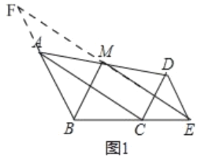
∵△CDE是等邊三角形
∴CD=CE=DE,∠CED=60°
∵∠ABC=120°
∴∠ABC+∠CED=180°
∵B、C、E三點共線
∴AB∥DE
∴∠F=∠DEM
∵點M是AD中點
∴AM=DM
又∵∠FMA=∠EMD
∴△AMF≌△DME
∴AF=DE=CE,FM=ME
∵AB=BC
∴BF=BE
∴BM⊥ME
(2)證明:如圖2,延長EM到點F,使MF=ME,連接BF,AF,,BE,
∵AM=DM,∠FMA=∠DME
∴△AMF≌△DMF
∴AF=DE=CE,∠FAD=ADE
在四邊形BADE中
∵∠BAD+∠ADE+∠DEB+∠EBA=360°
∵∠ABC=120°,∠CED=60°
∴∠CBE+∠CEB+∠BAD+∠ADE=180°
∵∠CBE+∠CEB+∠BCE=180°
∴∠BCE=∠BAD+∠ADE
∴∠BCE=∠BAF
∵AB=BC
∴△AFB≌△CEB
∴BF=BE,∠ABF=∠CBE
∴∠FBE=∠ABC=120°,∠BEF=30°
∴∠BME=90°,BE=2BM
在△ABC中
AB=AC=![]() ,∠ABC=120°
,∠ABC=120°
∴∠BAC=30°
過點B作BG⊥AC于點G
∴BG=![]() ,CG=AG=3
,CG=AG=3
∴EG=CG+CE=3+2=5
在Rt△BCE中,根據勾股定理得
![]()
∴![]()
(3)如圖3,延長EM到點F,使MF=ME,連接BF,AF,BM
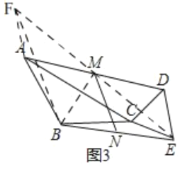
∵AM=DM,∠FMA=∠DME
∴△AMF≌△DMF
∴AF=DE=CE,∠FAD=∠ADE
在四邊形BADE中,
∵∠BAD+∠ADE+∠DEB+∠EBA=360°
∵∠ABC=120°,∠CED=60°
∴∠CBE+∠CEB+∠BAD+∠ADE=180°
∵∠CBE+∠CEB+∠BCE=180°
∴∠BCE=∠BAD+∠ADE
∴∠BCE=∠BAF
∵AB=BC
∴△AFB≌△CEB
∴BF=BE,∠ABF=∠CBE
∴∠FBE=∠ABC=120°,∠BEF=30°
∴∠BME=90°
∵點N是BE的中點
∴MN=![]() BE
BE
即:BE=2MN
在△BCE中,BC=![]() ,CE=CD=2
,CE=CD=2
∴![]()
∴![]()
∴![]()
故答案為:![]()


科目:初中數學 來源: 題型:
【題目】為了響應“足球進校國”的目標,興義市某學校開展了多場足球比賽在某場比賽中,一個足球被從地面向上踢出,它距地面的高度h(m)可以用公式h=﹣5t2+v0t表示,其中t(s)表示足球被踢出后經過的時間,v0(m/s)是足球被踢出時的速度,如果要求足球的最大高度達到20m,那么足球被踢出時的速度應該達到( )
A. 5m/s B. 10m/s C. 20m/s D. 40m/s
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于x的二次函數y1=x2+kx+k﹣1(k為常數)
(1)對任意實數k,函數圖象與x軸都有交點
(2)若當x≥75時,函數y的值都隨x的增大而增大,求滿足條件的最小整數k的值
(3)K取不同的值時,函數拋物線的頂點位置也會變化,但會在某一函數圖象上,求該函數圖象的解析式
(4)若當自變量x滿足0≤x≤3時,與其對應的函數值y的最小值為10,求此時k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某小區有一塊長為30m,寬為24m的矩形空地,計劃在其中修建兩塊相同的矩形綠地,它們的面積之和為480m2,兩塊綠地之間及周邊有寬度相等的人行通道,則人行通道的寬度為多少米?

查看答案和解析>>
科目:初中數學 來源: 題型:
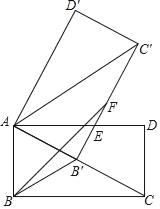
【題目】如圖,矩形ABCD中,AC=2AB,將矩形ABCD繞點A旋轉得到矩形AB′C′D′,使點B的對應點B'落在AC上,B'C'交AD于點E,在B'C′上取點F,使B'F=AB.
(1)求證:AE=C′E.
(2)求∠FBB'的度數.
(3)已知AB=2,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
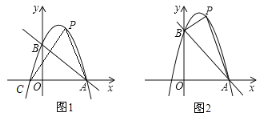
【題目】如圖,二次函數 y=ax 2 +bx+c 的圖象與 y 軸正半軸相交,其頂點坐標為(![]() ,1).下列結論:①abc<0;②a+b=0;③4ac-b2=4a;④a+b+c<0.其中正確的是( ).
,1).下列結論:①abc<0;②a+b=0;③4ac-b2=4a;④a+b+c<0.其中正確的是( ).

A.①②③④B.②③④C.①②③D.①②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 經過點
經過點![]() 和點
和點![]() .
.
(1)求此拋物線的函數表達式和直線![]() 的函數表達式;
的函數表達式;
(2)動點![]() 在第一象限內的拋物線上.
在第一象限內的拋物線上.
①如圖1,連接![]() ,
,![]() ,當
,當![]() 的面積和
的面積和![]() 的面積相等時,求出點
的面積相等時,求出點![]() 的橫坐標;
的橫坐標;
②如圖2,連接![]() ,求
,求![]() 的面積
的面積![]() 的最大值及此時點
的最大值及此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正比例函數y=kx(x≥0)與反比例函數 ![]() (x>0)的圖象交于點A(2,3)。
(x>0)的圖象交于點A(2,3)。
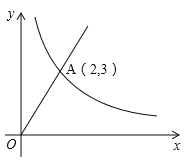
(1)求正比例函數與反比例函數的解析式;
(2)寫出正比例函數值大于反比例函數值時自變量x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com