Question

15．如果一個等腰三角形的三條邊長分別為1、1、$\sqrt{3}$，那么這個等腰三角形底角的度數(shù)為30°．

Answer 1

分析 過點A作AD⊥BC于D，由等腰三角形的性質(zhì)得出BD=$\frac{1}{2}$BC=$\frac{\sqrt{3}}{2}$，再根據(jù)余弦函數(shù)可得答案．

解答 解：如圖，過點A作AD⊥BC于D，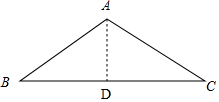

∵AB=AC=1，BC=$\sqrt{3}$，
∴BD=$\frac{1}{2}$BC=$\frac{\sqrt{3}}{2}$，
則cosB=$\frac{BD}{AB}$=$\frac{\sqrt{3}}{2}$，
∴∠B=30°，
故答案為：30°．

點評 本題主要考查等腰三角形的性質(zhì)及三角函數(shù)的定義、特殊角的三角函數(shù)值，熟練掌握等腰三角形的性質(zhì)和三角函數(shù)的定義是解題的關(guān)鍵．