
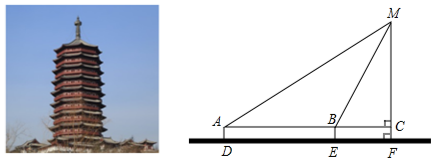
分析 設MC為xm,在Rt△BCM中,得到BC=$\frac{\sqrt{3}}{3}$x,在Rt△AMF中,得到AC=$\sqrt{3}$x,根據AC=AB+BC,列出方程即可解決問題.
解答 解:根據題意,得CF=BE=AD=1.5,AB=DE=40.
設MC為xm,在Rt△MCB中,tan∠1=$\frac{MC}{BC}$,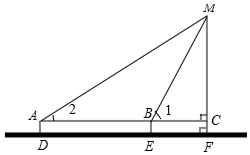
∴BC=$\frac{x}{tan60°}$=$\frac{\sqrt{3}}{3}$x,
同理可得AC=$\sqrt{3}$x,
∴$\sqrt{3}$x=$\frac{\sqrt{3}}{3}$x+40,
解得$x=20\sqrt{3}≈34.64$.…(4分)
∴MF=MC+CF≈34.64+1.5=36.14≈36.1(m)
答:古塔的高約為36.1米.
點評 本題考查解直角三角形,仰角俯角的應用等知識,解題的關鍵是學會利用參數構建方程解決問題,屬于中考常考題型.


 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 以Rt△ABC的直角頂點C為圓心,作一圓切斜邊AB于點T,過點A、B分別作⊙C的切線,E,D為切點,
以Rt△ABC的直角頂點C為圓心,作一圓切斜邊AB于點T,過點A、B分別作⊙C的切線,E,D為切點,查看答案和解析>>
科目:初中數學 來源: 題型:填空題
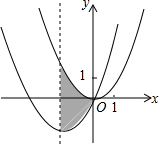 如圖,拋物線C1:y=$\frac{1}{2}$x2經過平移得到拋物線C2:y=$\frac{1}{2}$x2+2x,拋物線C2的對稱軸與兩段拋物線所圍成的陰影部分的面積是4.
如圖,拋物線C1:y=$\frac{1}{2}$x2經過平移得到拋物線C2:y=$\frac{1}{2}$x2+2x,拋物線C2的對稱軸與兩段拋物線所圍成的陰影部分的面積是4.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在△ABC中,AC⊥BC,∠B=30°,點E,F是線段AC的三等分點,點P是線段BC上的動點,點Q是線段AC上的動點,若AC=3,則四邊形EPQF周長的最小值是8.
如圖,在△ABC中,AC⊥BC,∠B=30°,點E,F是線段AC的三等分點,點P是線段BC上的動點,點Q是線段AC上的動點,若AC=3,則四邊形EPQF周長的最小值是8.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com