
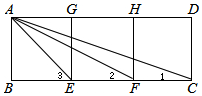
 如圖,四邊形ABEG、GEFH、HFCD都是邊長(zhǎng)相等的正方形
如圖,四邊形ABEG、GEFH、HFCD都是邊長(zhǎng)相等的正方形分析 (1)根據(jù)題意作出猜想即可;
(2)設(shè)正方形的邊長(zhǎng)為1,由正方形的性質(zhì)得出∠AEB=45°,AB=BE=EF=FC=1,∠B=90°,EC=2,由勾股定理求出AE=$\sqrt{2}$,證出 $\frac{AE}{EF}$=$\frac{EC}{AE}$,再由公共角∠AEF=∠CEA,得出△AEF∽△CEA,得出對(duì)應(yīng)角相等∠2=∠EAC,再由三角形的外角性質(zhì)即可得出結(jié)論.
解答 (1)解:猜想:∠1∠+2+∠3=90°.
故答案為:90;
(2)證明:設(shè)正方形的邊長(zhǎng)為1,
∵四邊形ABEG、GEFH、HFCD都是邊長(zhǎng)為1的正方形,
∴∠AEB=45°,AB=BE=EF=FC=1,∠B=90°,
∴EC=2a,AE=$\sqrt{2}$,
∵$\frac{AE}{EF}$=$\frac{\sqrt{2}}{1}$=$\sqrt{2}$,$\frac{EC}{AE}$=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
∴$\frac{AE}{EF}$=$\frac{EC}{AE}$.
又∵∠AEF=∠CEA,
∴△AEF∽△CEA,
∴∠2=∠EAC,
∵∠3=∠EAC+∠1=45°,
∴∠1∠+2+∠3=90°.
點(diǎn)評(píng) 本題考查了正方形的性質(zhì)、相似三角形的判定與性質(zhì),熟練掌握相似三角形的判定與性質(zhì),并能進(jìn)行推理論證與計(jì)算是解決問題的關(guān)鍵,屬于中考常考題型.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 問題:探究函數(shù)y=|x|-2的圖象與性質(zhì).
問題:探究函數(shù)y=|x|-2的圖象與性質(zhì).| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 1 | 0 | -1 | -2 | -1 | 0 | m | … |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| x | 1 | 2 | 3 | 4 | … |
| y | 0.6+3 | 0.6+6 | 0.6+9 | 0.6+12 | … |
| A. | y=0.6+x | B. | y=0.6+3x | C. | y=0.6×3+x | D. | y=0.6×3-x |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
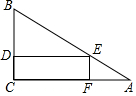 一塊三角形材料如圖所示,∠A=30°,∠C=90°,AB=12,用這塊材料剪出一個(gè)矩形CDEF,其中D、E、F分別在BC、AB、AC上.
一塊三角形材料如圖所示,∠A=30°,∠C=90°,AB=12,用這塊材料剪出一個(gè)矩形CDEF,其中D、E、F分別在BC、AB、AC上.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
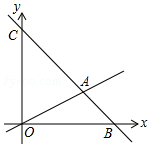 如圖,在平面直角坐標(biāo)系中,直線AB交x軸于點(diǎn)B(6,0),交y軸于點(diǎn)C(0,6),直線AB與直線OA:y=$\frac{1}{2}$x相交于點(diǎn)A,動(dòng)點(diǎn)M在線段OA和射線AC上運(yùn)動(dòng).
如圖,在平面直角坐標(biāo)系中,直線AB交x軸于點(diǎn)B(6,0),交y軸于點(diǎn)C(0,6),直線AB與直線OA:y=$\frac{1}{2}$x相交于點(diǎn)A,動(dòng)點(diǎn)M在線段OA和射線AC上運(yùn)動(dòng).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com