
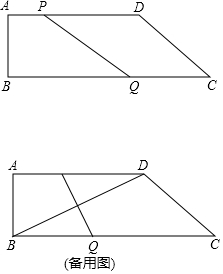
 如圖,在四邊形ABCD中,AD‖BC,∠B=90°,AB=4cm,AD=8cm,BC=14cm,點P從點A出發,以1cm/s的速度向點D運動;點Q從點C同時出發,以3cm/s的速度向點B運動,規定其中一個動點到達端點時,另一個端點也隨之停止運動.
如圖,在四邊形ABCD中,AD‖BC,∠B=90°,AB=4cm,AD=8cm,BC=14cm,點P從點A出發,以1cm/s的速度向點D運動;點Q從點C同時出發,以3cm/s的速度向點B運動,規定其中一個動點到達端點時,另一個端點也隨之停止運動.分析 (1)由當PQ∥CD時,四邊形PQCD為平行四邊形,可得方程8-t=3t,解此方程即可求得答案;
(2)根據PQ=CD,一種情況是:四邊形PQCD為平行四邊形,可得方程8-t=3t,一種情況是:四邊形PQCD為等腰梯形,可求得當QC-PD=QC-EF=QF+EC=2CE,即3t-(8-t)=12時,四邊形PQCD為等腰梯形,解此方程即可求得答案;
(3)當PQ垂直平分對角線BD時,得出四邊形BQDP是菱形,得出BQ=BP=PD=8-$\frac{3}{2}$t,在Rt△ABP中,由勾股定理得出方程,解方程求出t的值,得出BQ=5,求出CQ=9,即可得出Q點的速度.
解答 解:設運動時間為ts,根據題意得:PA=t,CQ=3t,
則PD=AD-PA=8-t.
(1)∵AD∥BC,
即PQ∥CD,
∴當PD=CQ時,四邊形PQCD為平行四邊形,
即8-t=3t,
解得:t=2,
即當t=2時,PQ∥CD;
(2)若PQ=DC,分兩種情況:
①PQ=DC,則四邊形PQCD是平行四邊形,由(1)可知,t=2,
②PQ=DC,則四邊形PQCD是等腰梯形,則QC=PD+2(BC-AD),
可得方程:3t=8-t+12,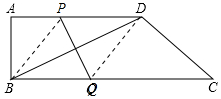
解得:t=5;
綜上所述:t為2s或5s時,PQ=CD.
(3)當PQ垂直平分對角線BD時,連接BP,DQ,
∵PD∥BC,
∴四邊形BQDP是菱形,
∴BQ=BP=PD=8-$\frac{3}{2}$t,
在Rt△ABP中,AP=$\frac{3}{2}$t,AB=4,
由勾股定理得:42+($\frac{3}{2}$t)2=(8-$\frac{3}{2}$t)2,
解得:t=2,
∴BQ=8-$\frac{3}{2}$×2=5,
∴CQ=14-5=9,
∴Q點的速度=9÷2=4.5(cm/s),
即Q點的速度是4.5cm/s時,PQ垂直平分對角線BD.
點評 此題是四邊形綜合題目,考查了直角梯形的性質、平行四邊形的判定、等腰梯形的判定以及全等三角形的判定與性質.此題綜合性強,有一定難度,注意掌握數形結合思想與分類討論思想的應用.


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:初中數學 來源: 題型:解答題
 如圖,AF是△ABC的高,點D、E分別在AB、AC上,且DE||BC,DE交AF于點G,設AD=5,AB=15,AC=12,GF=6.
如圖,AF是△ABC的高,點D、E分別在AB、AC上,且DE||BC,DE交AF于點G,設AD=5,AB=15,AC=12,GF=6.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| A | B | |
| 進價(萬元/.套) | 1.5 | 1.2 |
| 售價(萬元/套) | 1.65 | 1.4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 在矩形紙片ABCD中,AB=4,BC=10,E是AD邊的中點,把矩形紙片沿過點E的直線折疊,使點A落在BC邊上,則折痕EF的長為$\frac{5\sqrt{5}}{2}$.
在矩形紙片ABCD中,AB=4,BC=10,E是AD邊的中點,把矩形紙片沿過點E的直線折疊,使點A落在BC邊上,則折痕EF的長為$\frac{5\sqrt{5}}{2}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com