
 如圖,∠1+∠2=180°,∠A=∠C,BC平分∠EBD
如圖,∠1+∠2=180°,∠A=∠C,BC平分∠EBD分析 (1)根據同角的余角相等,可得∠BDC=∠1,進而得出AE∥CP;
(2)根據AE∥CP,可得∠C+∠ABC=180°,再根據∠A=∠C,可得∠A+∠ABC=180°,進而得出AD∥BC;
(3)根據BC平分∠EBD,可得∠3=∠4,再根據平行線的性質,可得∠3=∠C=∠5,∠4=∠6,進而得到∠5=∠6,即DA平分∠BDP.
解答 解:(1)AE與CP平行.
∵∠1+∠2=180°,∠2+∠CDB=180°,
∴∠BDC=∠1,
∴AE∥CP;
(2)AD與BC平行.
∵AE∥CP,
∴∠C+∠ABC=180°,
又∵∠A=∠C,
∴∠A+∠ABC=180°,
∴AD∥BC;
(3)DA平分∠BDP.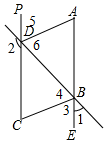
如圖所示,∵BC平分∠EBD,
∴∠3=∠4,
∵AD∥BC,AB∥CD,
∠3=∠C=∠5,∠4=∠6,
∴∠5=∠6,
∴DA平分∠BDP.
點評 本題主要考查了平行線的性質與判定的綜合運用,平行線的判定是由角的數量關系判斷兩直線的位置關系,平行線的性質是由平行關系來尋找角的數量關系.


科目:初中數學 來源: 題型:解答題
 如圖,在長為70米,寬為40米的長方形空地中,張老板想在上面修建焯天茶餐廳和子欣西餐廳,兩所餐廳的四周鋪上等寬的小路隔開,如果小路的面積占總面積的八分之一,求小路的寬度是多少?
如圖,在長為70米,寬為40米的長方形空地中,張老板想在上面修建焯天茶餐廳和子欣西餐廳,兩所餐廳的四周鋪上等寬的小路隔開,如果小路的面積占總面積的八分之一,求小路的寬度是多少?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
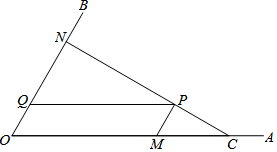 如圖,C為∠AOB的邊OA上一點,OC=6,N為邊OB上異于點O的一動點,P是線段CN上一點,過點P分別作PQ∥OA交OB于點Q,PM∥OB交OA于點M.
如圖,C為∠AOB的邊OA上一點,OC=6,N為邊OB上異于點O的一動點,P是線段CN上一點,過點P分別作PQ∥OA交OB于點Q,PM∥OB交OA于點M.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
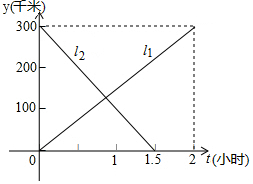 廈深鐵路開通后,直線l1與l2分別表示從深圳北開往潮陽站的動車和從潮陽站開往深圳的高鐵,兩車同時出發,設動車離深圳北的距離為y1(千米),高鐵離深圳的距離為距離y2(千米),行駛時間為t(小時),與t的函數關系如圖所示:
廈深鐵路開通后,直線l1與l2分別表示從深圳北開往潮陽站的動車和從潮陽站開往深圳的高鐵,兩車同時出發,設動車離深圳北的距離為y1(千米),高鐵離深圳的距離為距離y2(千米),行駛時間為t(小時),與t的函數關系如圖所示:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
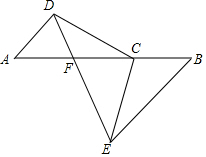 已知,如圖:C是AB上一點,點D,E分別在AB兩側,AD∥BE,且AD=BC,BE=AC.
已知,如圖:C是AB上一點,點D,E分別在AB兩側,AD∥BE,且AD=BC,BE=AC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知在⊙O中,AC是直徑,CB是⊙O的切線,連接AB,AB與⊙O交于點D,連接OD,CD,E為BC上一點,連接DE,且CE=DE.
如圖,已知在⊙O中,AC是直徑,CB是⊙O的切線,連接AB,AB與⊙O交于點D,連接OD,CD,E為BC上一點,連接DE,且CE=DE.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com