
 如圖,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,點O是AB的中點,點P在AB的延長線上,且BP=3.一動點E從O點出發,以每秒1個單位長度的速度沿OA勻速運動,到達A點后,立即以原速度沿AO返回;另一動點F從P點發發,以每秒1個單位長度的速度沿射線PA勻速運動,點E、F同時出發,當兩點相遇時停止運動,在點E、F的運動過程中,以EF為邊作等邊△EFG,使△EFG和矩形ABCD在射線PA的同側.設運動的時間為t秒(t≥0).
如圖,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,點O是AB的中點,點P在AB的延長線上,且BP=3.一動點E從O點出發,以每秒1個單位長度的速度沿OA勻速運動,到達A點后,立即以原速度沿AO返回;另一動點F從P點發發,以每秒1個單位長度的速度沿射線PA勻速運動,點E、F同時出發,當兩點相遇時停止運動,在點E、F的運動過程中,以EF為邊作等邊△EFG,使△EFG和矩形ABCD在射線PA的同側.設運動的時間為t秒(t≥0).分析 (1)當邊FG恰好經過點C時,由∠CFB=60°,得BF=3-t,在Rt△CBF中,根據三角函數求得t的值;
(2)根據運動的時間為t不同的取值范圍,求等邊△EFG和矩形ABCD重疊部分的面積為S的值,當0≤t<1時,重疊部分是直角梯形,面積S等于梯形的面積,
當1≤t<3時,重疊部分是S梯形MKFE-S△QBF,當3≤t<4時,重疊部分是S梯形MKFE,當4≤t<6時,重疊部分是正三角形的面積;
(3)當AH=AO=3時,AM=$\frac{1}{2}$AH=$\frac{3}{2}$,在Rt△AME中,由cos∠MAE=$\frac{AM}{AE}$,即cos30°=$\frac{\frac{3}{2}}{AE}$,得AE=$\sqrt{3}$,即3-t=$\sqrt{3}$或t-3=$\sqrt{3}$,求出t=3-$\sqrt{3}$或t=3+$\sqrt{3}$;
當AH=HO時,∠HOA=∠HAO=30°,又因為∠HEO=60°得到∠EHO=90°EO=2HE=2AE,再由AE+2AE=3,求出AE=1,即3-t=1或t-3=1,求出t=2或t=4;
當OH=OA=時∠HOB=∠OAH=30°,所以∠HOB=60°=∠HEB,得到點E和點O重合,從而求出t的值.
解答 解:(1)當等邊△EFG的邊FG恰好經過點C時,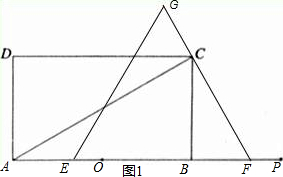
∠CFB=∠GFE=60°,∠BCF=30°,
∵BF=3-t,BC=2$\sqrt{3}$,
∴tan∠BCF=$\frac{BF}{BC}$,
即tan30°=$\frac{3-t}{2\sqrt{3}}$,
解得t=1
∴當等邊△EFG的邊FG恰好經過點C時,t=1;
(2)①如圖1,當0≤t<1時,作MN⊥AB于點N,
∵tan∠MEN=tan60°=$\frac{MN}{EN}$=$\frac{2\sqrt{3}}{EN}$,
∴EN=2,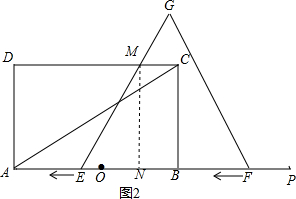
∵BE=BO+0E=3+t,EN=2,
∴CM=BN=BE-EN=3+t-2=t+1,
∴S=$\frac{1}{2}$(CM+BE)×BC=$\frac{1}{2}$(t+1+3+t)×2$\sqrt{3}$=2$\sqrt{3}$t+4$\sqrt{3}$.
②如圖2,當1≤t<3時,
∵EF=OP=6,
∴GH=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∵$\frac{MK}{EF}$=$\frac{GH-MN}{GH}$,
∴$\frac{MK}{6}$=$\frac{3\sqrt{3}-2\sqrt{3}}{3\sqrt{3}}$解得MK=2,
又∵BF=3-t,BQ=$\sqrt{3}$BF=$\sqrt{3}$(3-t),
∴S=S梯形MKFE-S△QBF,
=$\frac{1}{2}$(2+6)×2$\sqrt{3}$-$\frac{1}{2}$×(3-t)×$\sqrt{3}$×(3-t)
=-$\frac{\sqrt{3}}{2}$t2+3$\sqrt{3}$t+$\frac{7\sqrt{3}}{2}$.
③如圖3,當3≤t<4時
∵MN=2$\sqrt{3}$,EF=6-2(t-3)=12-2t,
∴GH=(12-2t)×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$-$\sqrt{3}$t,
∴$\frac{MK}{EF}=\frac{GH-MN}{GH}$,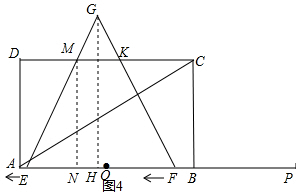
∴MK=8-2t,
S=-4$\sqrt{3}$t+20$\sqrt{3}$;
④如圖4,當4≤t<6時,
∵EF=12-2t,
高為:EF•sin60°=$\frac{\sqrt{3}}{2}$EF
S=$\sqrt{3}$t2-12$\sqrt{3}$t+36$\sqrt{3}$;
(3)存在t,使△AOH是等腰三角形.
理由如下:在Rt△ABC中,tan∠CAB=$\frac{BC}{AB}$=$\frac{\sqrt{3}}{3}$,
∴∠CAB=30°,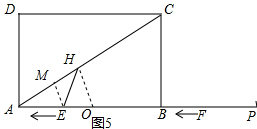
又∵∠HEO=60°,
∴∠HAE=∠AHE=30°,
∴AE=HE=3-t或t-3
①如圖5,
當AH=AO=3時,過點E作EM⊥AH于M,
則AM=$\frac{1}{2}$AH=$\frac{3}{2}$,
在Rt△AME中,cos∠MAE=$\frac{AM}{AE}$,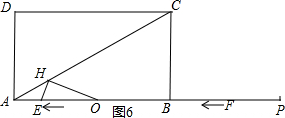
即cos30°=$\frac{\frac{3}{2}}{AE}$,
∴AE=$\sqrt{3}$,即3-t=$\sqrt{3}$或t-3=$\sqrt{3}$,
∴t=3-$\sqrt{3}$或t=3+$\sqrt{3}$.
②如圖6,
當HA=HO時,
則∠HOA=∠HAO=30°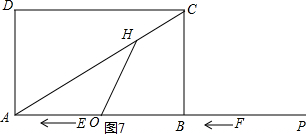
又∵∠HEO=60°,
∴∠EHO=90°,EO=2HE=2AE,
又∵AE+EO=3,
∴AE+2AE=3,AE=1,
即3-t=1或t-3=1,
∴t=2或t=4;
③如圖7,
當OH=OA時,
則∠OHA=∠OAH=30°
∴∠HOB=60°=∠HEB,
∴點E和點O重合,
∴AE=AO=3,
當E剛開始運動時3-t=3,
當點E返回O時是:t-3=3,
即3-t=3或t-3=3,t=6(舍去)或t=0;
,綜上,可得存在t,使△AOH是等腰三角形,此時t=3-$\sqrt{3}$、3+$\sqrt{3}$、2、4或0.
點評 此題主要考查了 平行四邊形的性質、平行四邊形的判定、矩形、矩形的性質、矩形的判定、菱形、菱形的性質、菱形的判定 等知識,關鍵是根據特殊三角形的性質,分類討論.


科目:初中數學 來源:2016-2017學年江蘇省東臺市第六教育聯盟七年級下學期第一次月考數學試卷 題型:填空題
一個等腰三角形的兩邊長分別是3cm和7cm,它的周長是____cm.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
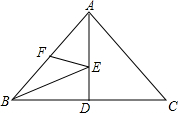 如圖,在△ABC中,AB=AC=5,BC=6,AD⊥BC于D,點E,F分別在AD,AB上,則BE+EF的最小值是( )
如圖,在△ABC中,AB=AC=5,BC=6,AD⊥BC于D,點E,F分別在AD,AB上,則BE+EF的最小值是( )| A. | 4 | B. | 4.8 | C. | 5 | D. | 5.4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,直線CD與直線AB相交于C,
如圖,直線CD與直線AB相交于C,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,小敏在測量學校一幢教學樓AB的高度時,她先在點C測得教學樓的頂部A的仰角為30°,然后向教學樓前進12米到達點D,又測得點A的仰角為45°.請你根據這些數據,求出這幢教學樓AB的高度.
如圖,小敏在測量學校一幢教學樓AB的高度時,她先在點C測得教學樓的頂部A的仰角為30°,然后向教學樓前進12米到達點D,又測得點A的仰角為45°.請你根據這些數據,求出這幢教學樓AB的高度.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com