
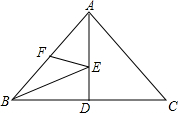
 如圖,在△ABC中,AB=AC=5,BC=6,AD⊥BC于D,點E,F分別在AD,AB上,則BE+EF的最小值是( )
如圖,在△ABC中,AB=AC=5,BC=6,AD⊥BC于D,點E,F分別在AD,AB上,則BE+EF的最小值是( )| A. | 4 | B. | 4.8 | C. | 5 | D. | 5.4 |
分析 作F關于AD的對稱點M,連接BM交AD于E,連接EF,過B作BN⊥AC于N,根據三線合一定理求出BD的長和AD平分∠BAC,根據勾股定理求出AD,根據三角形面積公式求出BN,根據對稱性質求出BE+EF=BM,根據垂線段最短得出BE+EF≥4.8,即可得出答案.
解答 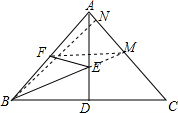 解:作F關于AD的對稱點M,連接BM交AD于E,連接EF,過B作BN⊥AC于N,
解:作F關于AD的對稱點M,連接BM交AD于E,連接EF,過B作BN⊥AC于N,
∵AB=AC=5,BC=6,AD⊥BC于D,
∴BD=DC=3,AD平分∠BAC,
∴M在AC上,
在Rt△ABD中,由勾股定理得:AD=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴S△ABC=$\frac{1}{2}$×BC×AD=$\frac{1}{2}$×AC×BN,
∴BN=$\frac{BC×AD}{AC}$=$\frac{6×4}{5}$=4.8,
∵F關于AD的對稱點M,
∴EF=EM,
∴BE+EF=BE+EM=BM,
根據垂線段最短得出:BM≥BN,
即BE+EF≥4.8,
即BF+EF的最小值是4.8,
故選B.
點評 此題主要考了等腰三角形的性質,勾股定理,軸對稱-最短路線問題等知識點的理解和掌握,能求出BE+EF=BM的長是解此題的關鍵.題目具有一定的代表性,是一道比較好的題目.


 一線名師權威作業本系列答案
一線名師權威作業本系列答案科目:初中數學 來源:2016-2017學年廣東省七年級下學期第一次月考數學試卷(解析版) 題型:單選題
已知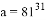 ,
,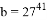 ,
,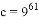 ,則
,則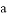 、
、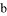 、
、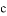 的大小關系是( )
的大小關系是( )
A. 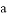 >
>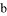 >
>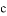 B.
B. 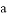 >
>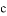 >
>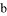 C.
C. 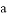 <
<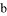 <
<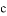 D.
D. 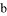 >
>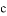 >
>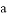
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在平面直角坐標系中,點 A(-2,0),B(2,0),C(0,2),點 D,點E分別是 AC,BC的中點,將△CDE繞點C逆時針旋轉得到△CD′E′,及旋轉角為α,連接 AD′,BE′.
在平面直角坐標系中,點 A(-2,0),B(2,0),C(0,2),點 D,點E分別是 AC,BC的中點,將△CDE繞點C逆時針旋轉得到△CD′E′,及旋轉角為α,連接 AD′,BE′.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,點O是AB的中點,點P在AB的延長線上,且BP=3.一動點E從O點出發,以每秒1個單位長度的速度沿OA勻速運動,到達A點后,立即以原速度沿AO返回;另一動點F從P點發發,以每秒1個單位長度的速度沿射線PA勻速運動,點E、F同時出發,當兩點相遇時停止運動,在點E、F的運動過程中,以EF為邊作等邊△EFG,使△EFG和矩形ABCD在射線PA的同側.設運動的時間為t秒(t≥0).
如圖,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,點O是AB的中點,點P在AB的延長線上,且BP=3.一動點E從O點出發,以每秒1個單位長度的速度沿OA勻速運動,到達A點后,立即以原速度沿AO返回;另一動點F從P點發發,以每秒1個單位長度的速度沿射線PA勻速運動,點E、F同時出發,當兩點相遇時停止運動,在點E、F的運動過程中,以EF為邊作等邊△EFG,使△EFG和矩形ABCD在射線PA的同側.設運動的時間為t秒(t≥0).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (a+3)2(a-3) | B. | (a+3)2 | C. | (a+3)(a-3) | D. | (a-3)2(a+3)2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 75000名學生是總體 | |
| B. | 1000名學生的視力是總體的一個樣本 | |
| C. | 每名學生是總體的一個個體 | |
| D. | 上述調查是普查 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com