

分析 (1)先求得tan∠A=2.從而得到PA=t,PD=QP=2t,最后依據PA+PN=4列方程求解即可;
(2)①當0<t<$\frac{2}{3}$時,EN=AE-PA-PN;當$\frac{2}{3}$≤t<2時,EN=AN-AE=PA+PN-AE;當t≥2時,EN=AP+PN-AE;
(3)①當0<t≤$\frac{4}{3}$時,S=正方形的面積;②當$\frac{4}{3}$<t≤2時.S=S正方形PQMN-S△FND;當2<t≤4時,S=梯形PQCD的面積;當4<t≤6時,S=△CQF的面積;當t>6時,S=0;
(4)如圖9所示:建立坐標系可得到Q(2-t,2t,),M(2-3t,2t),然后分為OM=OQ,MO=MQ,QO=QM三種情況,接下來依據兩點間的距離公式列方程求解即可;如圖10所示:當Q在BC上時,MQ=QO=4,在Rt△BOQ中,依據勾股定理可求得QB的長,然后可求得t的值
解答 解:(1)如圖1所示:
∵E是AD的中點,AD=4,
∴AE=2.
∵AE=2,BE=4,∠BEA=90°,
∴tan∠A=2.
又∵PA=t,
∴QP=2t.
∵PQMN為正方形,
∴PD=2t.
∴t+2t=4.
解得:t=$\frac{4}{3}$.
(2)①當0<t<$\frac{2}{3}$時,如圖2所示:
∵由(1)可知PA=t,NP=2t.
∴EN=AE-PA-PN=2-t-2t=2-3t.
當$\frac{2}{3}$≤t<2時,如圖3所示:
∵由(1)可知PA=t,NP=2t.
∴EN=AN-AE=PA+PN-AE=t+2t-2=3t-2.
當t≥2時,如圖4所示: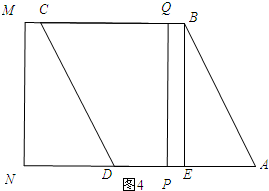
∵PA=t,PN=4,
∴EN=AP+PN-AE=t+4-2=t+2.
綜上所述,EN=$\left\{\begin{array}{l}{2-3t(0<t<\frac{2}{3})}\\{3t-2(\frac{2}{3}≤t<2)}\\{t+2(t≥2)}\end{array}\right.$.
(3)①如圖5所示:
當0<t≤$\frac{4}{3}$時,S=(2t)2=4t2;
②如圖6所示:當$\frac{4}{3}$<t≤2時.
∵NA=3t,AD=4,
∴DN=3t-4.
∴FN=2ND=2(3t-4).
∴S=S正方形PQMN-S△FND=(2t)2-$\frac{1}{2}$×2×(3t-4)2=-5t2+24t-16.
當2<t≤4時,如圖7所示:
∵CQ=CB+EA-PA=6-t,DP=AD-AP=4-t,
∴S=$\frac{1}{2}$×4×(6-t+4-t)=-4t+20.
當4<t≤6時,如圖8所示: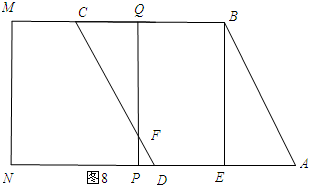
∵CQ=6-t,
∴QF=12-2t.
∴S=$\frac{1}{2}$CQ•QF=$\frac{1}{2}$×2×(6-t)2=t2-12t+36.
當t>6時,S=0.
綜上所述S與t的函數為S=$\left\{\begin{array}{l}{4{t}^{2}(0<t≤\frac{4}{3})}\\{-5{t}^{2}+24t-16(\frac{4}{3}<t≤2)}\\{-4t+20(2<t≤4)}\\{{t}^{2}-12t+36(4<t≤6)}\\{0(t>2)}\end{array}\right.$.
(4)如圖9所示: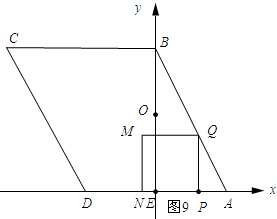
∵PA=t,PQ=QM=2t,
∴Q(2-t,2t,),M(2-3t,2t).
當OM=OQ時,由兩點間的距離公式可知:(2-3t)2+(2-2t)2=(2-t)2+(2-2t)2.
整理得:-2t(4-4t)=0.
解得:t=1或t=0(舍去).
當MO=MQ時.(2-3t)2+(2-2t)2=(2t)2.
整理得:9t2-20t+8=0.
解得:t=$\frac{10+2\sqrt{7}}{9}$或t=$\frac{10-2\sqrt{7}}{9}$.
當QO=QM時(2-t)2+(2-2t)2=(2t)2.
整理得:t2-12t+8=0.
解得:t=6-2$\sqrt{7}$,t=6+2$\sqrt{7}$(舍去).
如圖10所示:當MQ=QO=4時.
∵在Rt△BOQ中,QB=$\sqrt{Q{O}^{2}-O{B}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
∴PA+QB+EA=2$\sqrt{3}$+2即t=2+2$\sqrt{3}$.
綜上所述,當t=2+2$\sqrt{3}$或t=6-2$\sqrt{7}$或t=$\frac{10+2\sqrt{7}}{9}$或t=$\frac{10-2\sqrt{7}}{9}$時,△MQO為等腰三角形.
點評 本題主要考查的是四邊形的綜合應用,解答本題主要應用了銳角三角形函數的定義、正方形的性質、正方形的面積、梯形的面積、三角形的面積,等腰三角形的定義,兩點間的距離公式、一元二次方程、一元一次方程的解法,根據題意畫出符合題意的圖形是解題的關鍵.


 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案 一線名師權威作業本系列答案
一線名師權威作業本系列答案科目:初中數學 來源:2016-2017學年江西省下期九年級第一次月考數學試卷(解析版) 題型:判斷題
在平面直角坐標系xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如圖的方式放置.點A1,A2,A3,…,An和點C1,C2,C3,…,Cn分別落在直線y=x+1和x軸上.拋物線L1過點A1,B1,且頂點在直線y=x+1上,拋物線L2過點A2,B2,且頂點在直線y=x+1上,…,按此規律,拋物線Ln過點An,Bn,且頂點也在直線y=x+1上,其中拋物線L2交正方形A1B1C1O的邊A1B1于點D1,拋物線L3交正方形A2B2C2C1的邊A2B2于點D2,…,拋物線Ln+1交正方形AnBnCnCn-1的邊AnBn于點Dn(其中n≥2且n為正整數).
(1)直接寫出下列點的坐標:B1________,B2________,B3________;
(2)寫出拋物線L2、L3的解析式,并寫出其中一個解析式求解過程,再猜想拋物線Ln的頂點坐標
(3)設A1D1=k1·D1B1,A2D2=k2·D2B2,試判斷k1與k2的數量關系并說明理由.

查看答案和解析>>
科目:初中數學 來源:2016-2017學年廣東省七年級下學期第一次月考數學試卷(解析版) 題型:單選題
已知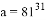 ,
,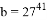 ,
,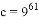 ,則
,則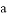 、
、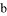 、
、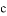 的大小關系是( )
的大小關系是( )
A. 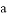 >
>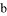 >
>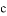 B.
B. 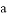 >
>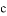 >
>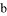 C.
C. 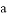 <
<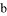 <
<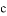 D.
D. 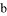 >
>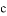 >
>
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
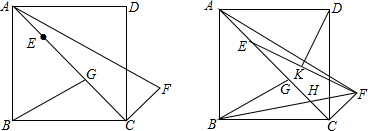
 在平面直角坐標系中,點 A(-2,0),B(2,0),C(0,2),點 D,點E分別是 AC,BC的中點,將△CDE繞點C逆時針旋轉得到△CD′E′,及旋轉角為α,連接 AD′,BE′.
在平面直角坐標系中,點 A(-2,0),B(2,0),C(0,2),點 D,點E分別是 AC,BC的中點,將△CDE繞點C逆時針旋轉得到△CD′E′,及旋轉角為α,連接 AD′,BE′.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,點O是AB的中點,點P在AB的延長線上,且BP=3.一動點E從O點出發,以每秒1個單位長度的速度沿OA勻速運動,到達A點后,立即以原速度沿AO返回;另一動點F從P點發發,以每秒1個單位長度的速度沿射線PA勻速運動,點E、F同時出發,當兩點相遇時停止運動,在點E、F的運動過程中,以EF為邊作等邊△EFG,使△EFG和矩形ABCD在射線PA的同側.設運動的時間為t秒(t≥0).
如圖,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,點O是AB的中點,點P在AB的延長線上,且BP=3.一動點E從O點出發,以每秒1個單位長度的速度沿OA勻速運動,到達A點后,立即以原速度沿AO返回;另一動點F從P點發發,以每秒1個單位長度的速度沿射線PA勻速運動,點E、F同時出發,當兩點相遇時停止運動,在點E、F的運動過程中,以EF為邊作等邊△EFG,使△EFG和矩形ABCD在射線PA的同側.設運動的時間為t秒(t≥0).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com