
分析 首先求出AB的長,再連圓心和各切點,利用切線長定理用半徑表示AF和BF,而它們的和等于AB,得到關于r的方程,解方程求出半徑,再求出圓的面積即可.
解答 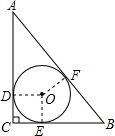 解:連OD,OE,OF,如圖所示,
解:連OD,OE,OF,如圖所示,
設半徑為r.則OE⊥BC,OF⊥AB,OD⊥AC,CD=r.
∵∠C=90°,BC=5cm,AC=12cm,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=13cm,
∴BE=BF=(5-r)cm,AF=AD=(12-r)cm,
∴5-r+12-r=13,
∴r=2.即Rt△ABC的內切圓半徑為2cm
∴△ABC的內切圓⊙O的面積=π×22=4π(cm2),
故答案為:4πcm2.
點評 此題主要考查了勾股定理以及直角三角形內切圓半徑求法等知識,熟練掌握切線長定理和勾股定理.此題讓我們記住一個結論:直角三角形內切圓的半徑等于兩直角邊的和與斜邊的差的一半.


 一線名師提優試卷系列答案
一線名師提優試卷系列答案 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com