
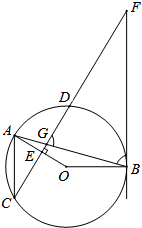
 如圖,在⊙O中,弦AB與弦CD相交于點(diǎn)G,OA⊥CD于點(diǎn)E,過點(diǎn)B的直線與CD的延長線交于點(diǎn)F,AC∥BF.
如圖,在⊙O中,弦AB與弦CD相交于點(diǎn)G,OA⊥CD于點(diǎn)E,過點(diǎn)B的直線與CD的延長線交于點(diǎn)F,AC∥BF.分析 (1)由OA=OB,得出∠OAB=∠OBA,由OA⊥CD,得出∠OAB+∠AGC=90°,推出∠FBG+∠OBA=90°,即∠OBF=90°,即可得出結(jié)論;
(2)由平行線得出∠ACF=∠F,求出CE=$\frac{1}{2}$CD=12,得出tan∠ACF=$\frac{AE}{CE}$=$\frac{3}{4}$,求出AE=9,連接OC,設(shè)圓的半徑為r,則OE=r-9,由勾股定理得出方程,解方程即可;
(3)連接BD,證明△BDG∽△FBG,得出對應(yīng)邊成比例$\frac{DG}{GB}=\frac{GB}{GF}$,得出GB2=DG•GF,即可得出結(jié)果.
解答 (1)證明:∵OA=OB,
∴∠OAB=∠OBA,
∵OA⊥CD,
∴∠OAB+∠AGC=90°,
又∵∠FGB=∠FBG,∠FGB=∠AGC,
∴∠FBG+∠OBA=90°,即∠OBF=90°,
∴OB⊥FB,
∵AB是⊙O的弦,
∴點(diǎn)B在⊙O上,
∴BF是⊙O的切線;
(2)解:∵AC∥BF,
∴∠ACF=∠F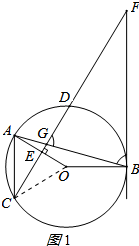 ∵CD=24,OA⊥CD,
∵CD=24,OA⊥CD,
∴CE=$\frac{1}{2}$CD=12,
∵tan∠F=$\frac{3}{4}$,
∴tan∠ACF=$\frac{AE}{CE}$=$\frac{3}{4}$,
即$\frac{AE}{12}=\frac{3}{4}$,
解得AE=9,
連接OC,如圖1所示:
設(shè)圓的半徑為r,則OE=r-9,
在Rt△OCE中,CE2+OE2=OC2,
即122+(r-9)2=r2,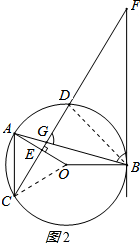
解得:r=12.5;
(3)解:是定值$\frac{{\sqrt{2}}}{2}$;理由如下:
連接BD,如圖2所示:
∵∠DBG=∠ACF,∠ACF=∠F,
∴∠DBG=∠F,
∵∠DGB=∠FGB,
∴△BDG∽△FBG,
∴$\frac{DG}{GB}=\frac{GB}{GF}$,
即GB2=DG•GF,
∴$\frac{G{F}^{2}-G{B}^{2}}{\sqrt{2}DF•GF}$=$\frac{G{F}^{2}-DG•GF}{\sqrt{2}DF•GF}$=$\frac{GF(GF-DG)}{\sqrt{2}DF•GF}$=$\frac{GF•DF}{\sqrt{2}DF•GF}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
點(diǎn)評 本題是圓的綜合題目,考查了切線的判定、圓周角定理、等腰三角形的性質(zhì)、平行線的性質(zhì)、勾股定理、三角函數(shù)、相似三角形的判定與性質(zhì)等知識;本題綜合性強(qiáng),有一定難度,證明三角形相似是解決問題(3)的關(guān)鍵.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
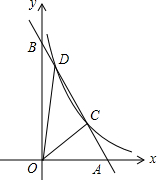 如圖,已知直線y1=ax+b與x軸、y軸分別交于A、B兩點(diǎn),與雙曲線y2=$\frac{k}{x}$(x>0)交于C(m,n)、D(p,q)兩點(diǎn),連接OC、OD.
如圖,已知直線y1=ax+b與x軸、y軸分別交于A、B兩點(diǎn),與雙曲線y2=$\frac{k}{x}$(x>0)交于C(m,n)、D(p,q)兩點(diǎn),連接OC、OD.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
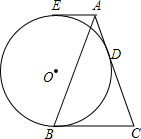 如圖,在△ABC中,AB=AC,半徑為4的⊙O分別與直線BC,AC相切于點(diǎn)B,D,過點(diǎn)A作⊙O的切線,E為切點(diǎn),當(dāng)AE∥BC時,AE的長是2$\sqrt{2}$.
如圖,在△ABC中,AB=AC,半徑為4的⊙O分別與直線BC,AC相切于點(diǎn)B,D,過點(diǎn)A作⊙O的切線,E為切點(diǎn),當(dāng)AE∥BC時,AE的長是2$\sqrt{2}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
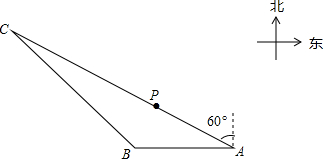 如圖.有一艘漁船P在捕魚作業(yè)時出現(xiàn)故障,急需搶修,調(diào)度中心通知附近兩個小島A,B上的觀測點(diǎn)進(jìn)行觀測,從觀測站A測得漁船P在北偏西60°的方向,同時測得搜救船C也在北偏西60°的方向,從觀測站B測得漁船P在北偏東32°的方向,測得搜救船C在北偏西45°方向,已知觀測站A在觀測站B東40里處,問搜救船C與漁船P的距離是多少?(結(jié)果保留整數(shù),參考數(shù)據(jù):sin32°≈0.53,cos32°≈0.85;tan32°≈0.62,sin58°≈0.85;cos58°≈0.53;tan58°≈1.60;$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).
如圖.有一艘漁船P在捕魚作業(yè)時出現(xiàn)故障,急需搶修,調(diào)度中心通知附近兩個小島A,B上的觀測點(diǎn)進(jìn)行觀測,從觀測站A測得漁船P在北偏西60°的方向,同時測得搜救船C也在北偏西60°的方向,從觀測站B測得漁船P在北偏東32°的方向,測得搜救船C在北偏西45°方向,已知觀測站A在觀測站B東40里處,問搜救船C與漁船P的距離是多少?(結(jié)果保留整數(shù),參考數(shù)據(jù):sin32°≈0.53,cos32°≈0.85;tan32°≈0.62,sin58°≈0.85;cos58°≈0.53;tan58°≈1.60;$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com