
分析 (1)根據閱讀知識找到規律即可求解;
(2)原式變形為-$\frac{1}{3}$(-2-1)×[(-2)2014+(-2)2013+(-2)2012+(-2)2011+(-2)2010…+(-2)3+(-2)2+(-2)+1],計算即可得到結果.
解答 解:(1)(x-1)×(xn+xn-1+…+x+1)=xn+1-1(n為正整數);
(2)22014-22013+22012-22011+22010…-23+22-2+1
=-$\frac{1}{3}$×(-2-1)×[(-2)2014+(-2)2013+(-2)2012+(-2)2011+(-2)2010…+(-2)3+(-2)2+(-2)+1]
=-$\frac{1}{3}$×[(-2)2015-1]
=$\frac{{2}^{2015}+1}{3}$.
故答案為:xn+1-1;$\frac{{2}^{2015}+1}{3}$.
點評 此題考查了平方差公式,弄清題中的規律是解本題的關鍵.


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
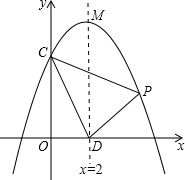 如圖:拋物線y=ax2+bx+c交y軸于點C(0,4),對稱軸x=2與x軸交于點D,頂點為M,且DM=OC+OD,
如圖:拋物線y=ax2+bx+c交y軸于點C(0,4),對稱軸x=2與x軸交于點D,頂點為M,且DM=OC+OD,查看答案和解析>>
科目:初中數學 來源: 題型:填空題
| 型號 | A | B |
| 單個盒子容量(升) | 2 | 3 |
| 單價(元) | 5 | 6 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com