在平面直角坐標系中，已知點A（﹣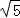
，0），B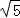（，0），點C在坐標軸上，且AC+BC=6，寫出滿足條件的所有點C的坐標
閱讀快車系列答案科目：初中數學 來源： 題型：
如圖，（1）△ABC是斜邊AB的長為3的等腰直角三角形，在△ABC內作第1個內接正方形A1B1D1E1（D1、E1在AB上，A1、B1分別在AC、BC上），再在△A1B1C內用同樣的方法作第2個內接正方形A2B2D2E2，…如此下去，操作n次，則第一個內接正方形的邊長是 ，第n個小正方形AnBnDnEn 的邊長是 _________ ．
（2）在△ABC中，BC=12，高AD=8，四邊形PQMN為△ABC的內接矩形，（P在AB上，Q在AC上，M、N在BC上），
①求當PQ為何值時，矩形PQMN面積最大。
②若再在△APQ中作一個內接矩形P2Q2M2N2，如此下去，操作n次，求PnQn的長。（直接寫出結果）
(3)解完上述兩題，根據其中一題你還能歸納出怎樣的數學結論，請簡單的寫出一條。
查看答案和解析>>
科目：初中數學 來源： 題型：
四邊形ABCD中，對角線AC、BD相交于點O，下列條件不能判定這個四邊形是平行四邊形的是（ ）
A．AB∥DC，AD∥BC B．AD∥BC ∠ABC=∠ADC
C．AO=CO，BO=DO D．AB∥DC，AD=BC
查看答案和解析>>
科目：初中數學 來源： 題型：
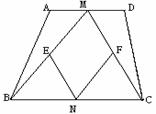
如圖，在等腰梯形ABCD中，M、N分別為AD、BC的中點，E、F分別為BM、CM的中點。
（1）求證：△ABM≌△CDM；
（2）判斷并證明四邊形MENF是何種特殊的四邊形；
‚當等腰梯形ABCD的高h與底邊BC滿足怎樣的數量關系時，四邊形MENF是正方形？（直接寫出結論，不需要證明）．
查看答案和解析>>
科目：初中數學 來源： 題型：
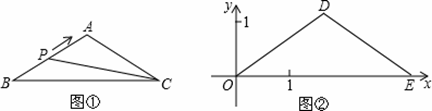
如圖①，在△ABC中，AB=AC，BC=acm，∠B=30°．動點P以1cm/s的速度從點B出發，沿折線B-A-C運動到點C時停止運動．設點P出發x s時，△PBC的面積為y cm2．已知y與x的函數圖象如圖②所示．請根據圖中信息，解答下列問題：
（1）試判斷△DOE的形狀，并說明理由；
（2）當a為何值時，△DOE與△ABC相似？
查看答案和解析>>
科目：初中數學 來源： 題型：
有下面3個結論: ① 存在兩個不同的無理數, 它們的積是整數； ② 存在兩個不同的無理數, 它們的差是整數； ③ 存在兩個不同的非整數的有理數, 它們的和與商都是整數. 先判斷這3個結論分別是正確還是錯誤的, 如果正確, 請舉出符合結論的兩個數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
a3by與﹣5a2yb4是同類項，則這兩個同類項合并的結果是 
·(m2－1)的結果是( )A．－m2－2m－1 B．－m2＋2m－1 C．m2－2m－1 D．m2－1